
题目列表(包括答案和解析)
(本小题满分14分)已知定义在 上的函数
上的函数 ,满足条件:①
,满足条件:①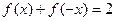 ,②对非零实数
,②对非零实数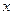 ,都有
,都有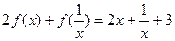 .
.
(1)求函数 的解析式;
的解析式;
(2)设函数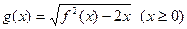 ,直线
,直线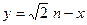 分别与函数
分别与函数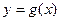 ,
,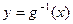 交于
交于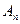 、
、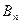 两点,(其中
两点,(其中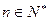 );设
);设 ,
,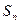 为数列
为数列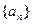 的前
的前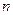 项和,求证:当
项和,求证:当 时,
时,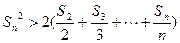 .
.
(本小题满分14分)
已知函数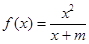 的图像经过点
的图像经过点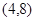 .
.
(1)求该函数的解析式;
(2)数列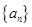 中,若
中,若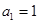 ,
,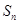 为数列
为数列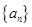 的前
的前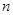 项和,且满足
项和,且满足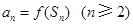 ,
,
证明数列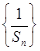 成等差数列,并求数列
成等差数列,并求数列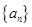 的通项公式;
的通项公式;
(3)另有一新数列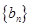 ,若将数列
,若将数列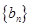 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
|
|
|
|
|
|
|
|
记表中的第一列数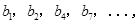 构成的数列即为数列
构成的数列即为数列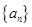 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
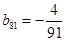 时,求上表中第
时,求上表中第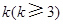 行所有项的和.
行所有项的和.
(本小题满分14分) 对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(本小题满分14分)已知定义在 上的函数
上的函数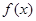 ,满足条件:①
,满足条件:① ,②对非零实数
,②对非零实数 ,都有
,都有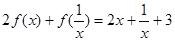 .
.
(1)求函数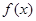 的解析式;
的解析式;
(2)设函数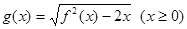 ,直线
,直线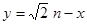 分别与函数
分别与函数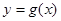 ,
,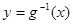 交于
交于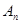 、
、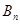 两点,(其中
两点,(其中 );设
);设 ,
,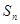 为数列
为数列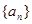 的前
的前 项和,求证:当
项和,求证:当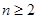 时,
时,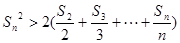 .
.
(本小题满分14分)
设二次函数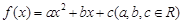 满足下列条件:
满足下列条件:
①当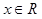 时,其最小值为0,且
时,其最小值为0,且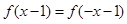 成立;
成立;
②当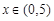 时,
时,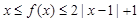 恒成立.
恒成立.
(1)求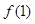 的值;
的值;
(2)求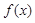 的解析式;
的解析式;
(3)求最大的实数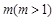 ,使得存在
,使得存在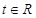 ,只要当
,只要当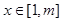 时,就有
时,就有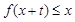 成立
成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com