宇航员在某一星球表面上做摆球实验．用不可伸长的轻质细线悬挂一个可视为质点的小球，细线长为L，细线端点悬于O点，摆线初始时与竖直方向夹角为θ，θ小于90°．现无初速释放小球、不计阻力，测得小球经过最低位置时的速度大小为v₀．已知该星球的半径为R、万有引力常量为G
（1）求出该星球表面附近的重力加速度g．
（2）求出该星球的质量M．

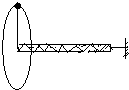我们学习了“用单摆测定重力加速度”，其实测定重力加速度的方法还很多，比如下面就是一宇航员到达某一星球后，做的一个测定该星球表面重力加速度的实验：取一根细线穿过光滑的细直管，细线一端拴一质量为m的砝码，另一端连接在一固定的测力计上，手握细直管抡动砝码，使它在竖直平面内做完整的圆周运动，停止抡动细直管，砝码可继续在同一竖直平面内做完整的圆周运动，如图，此时观察测力计得到当砝码运动到圆周的最低点和最高点两位置时测力计的读数差为△F，则由测量结果可得该星球表面重力加速度g=，若已知星球半径R，则星球质量为（已知万有引力常量为G）