
题目列表(包括答案和解析)
(本小题满分13分)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,……,依次类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第![]() 层第
层第![]() 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为![]() .(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
.(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
(Ⅰ)求![]() 的值,并猜想
的值,并猜想![]() 的表达式.(不必证明)
的表达式.(不必证明)
 (Ⅱ)设小弹子落入第6层第
(Ⅱ)设小弹子落入第6层第![]() 个竖直通道得到分数为
个竖直通道得到分数为![]() ,
,
其中![]() ,试求
,试求![]() 的分布列及数学期望.
的分布列及数学期望.
()本小题满分13分
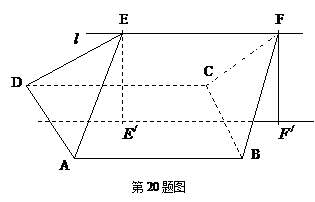 如图,ABCD的边长为2的正方形,直线
如图,ABCD的边长为2的正方形,直线![]() 与平面ABCD平行,E和F式
与平面ABCD平行,E和F式![]() 上的两个不同点,且EA=ED,FB=FC,
上的两个不同点,且EA=ED,FB=FC, ![]() 和
和![]() 是平面ABCD内的两点,
是平面ABCD内的两点,![]() 和
和![]() 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线![]() 垂直且平分线段AD:
垂直且平分线段AD:
(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面
体ABCDEF的体积。
(本小题满分13分)如图,抛物线的顶点在坐标原点,且开口向右,点A,B,C在抛物线上,△ABC的重心F为抛物线的焦点,直线AB的方程为![]() .(Ⅰ)求抛物线的方程;(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由.
.(Ⅰ)求抛物线的方程;(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由.
(本小题满分13分)
如图,矩形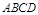 所在的平面与平面
所在的平面与平面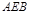 垂直,且
垂直,且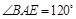 ,
,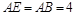 ,
,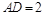 ,
,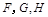 分别为
分别为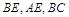 的中点.
的中点.

(Ⅰ) 求证:直线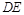 与平面
与平面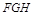 平行;
平行;
(Ⅱ)若点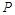 在直线
在直线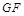 上,且二面角
上,且二面角 的大小为
的大小为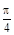 ,试确定点
,试确定点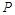 的位置.
的位置.
(本小题满分13分)如图,在直三棱柱ABC—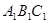 中,
中,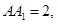 AB = 1,
AB = 1,
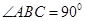 ;点D、E分别在
;点D、E分别在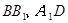 上,且
上,且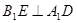 ,
,
四棱锥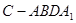 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与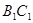 的距离;(8分)
的距离;(8分)
(2)若BC =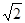 ,求二面角
,求二面角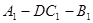 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com