练习册

  • 练习册
  • 试题
    3．数列的分类: 按项分类:有穷数列,无穷数列, 【查看更多】

     

    题目列表(包括答案和解析)

    现有6本不同的书，按下列要求各有多少种不同的分法：

    （I）分为三份，每份2本；

    （II）分给甲、乙、丙三人每人2本；

    （III）分给甲、乙、丙三人；

    （IV）分给甲、乙、丙三人，每人至少1本.

    （最后结果请用数字表示）.

     

    查看答案和解析>>

    数列{an}的前n项和是Sn，若数列{an}的向若按如下规律排列：
    1
    2
    ，
    1
    3
    ，
    2
    3
    ，
    1
    4
    ，
    2
    4
    ，
    3
    4
    ，
    1
    5
    ，
    2
    5
    ，
    3
    5
    ，
    4
    5
    ，
    1
    6
    ，…    ，若存在正整数k，使Sk＜10，Sk+1≥10，则ak=（　　）

    查看答案和解析>>

    已知等比数列{an}的公比q＞1，且a1与a4的一等比中项为4
    		2
    ，a2与a3的等差中项为6．
    （I）求数列{an}的通项公式；
    （Ⅱ）设Sn为数列{an}的前n项和，bn=Sn+3+（-1）n+1an2（n∈N*），请比较bn与bn+1的大小；
    （Ⅲ）数列{an}中是否存在三项，按原顺序成等差数列？若存在，则求出这三项；若不存在，则加以证明．

    查看答案和解析>>

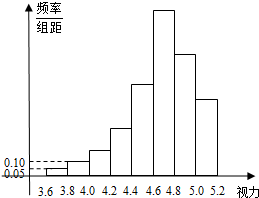    为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力，按视力情况分成8组，得到如图所示的频率分布直方图，但不慎将部分数据丢失，只知道前6组的频数从左到右依次是等比数列{an}的前六项，后3组的频数从左到右依次是等差数列{bn}的前三项．
    （1）求数列{an}和{bn}的通项公式；
    （2）设数列{cn}满足cn=
    35-bn3an
    ，求数列{cn}的前n项和Sn．

    查看答案和解析>>

    正整数数列{an}满足：a1=1，an+1=
    an-n，an＞n
    an+n，an≤n.

    （Ⅰ）写出数列{an}的前5项；
    （Ⅱ）将数列{an}中所有值为1的项的项数按从小到大的顺序依次排列，得到数列{nk}，试用nk表示nk+1（不必证明）；
    （Ⅲ）求最小的正整数n，使an=2013．

    查看答案和解析>>


    同步练习册答案