．（本小题满分10分）

如图，已知扇形的半径为15cm，∠AOB=120°。

 

1.（1）求扇形的面积；

2.（2）用这扇形围成圆锥的侧面，求该圆锥的高和底面半径。

 

（本小题满分10分）
在图15-1至图15-3中，直线MN与线段AB相交于点O，∠1 = ∠2 = 45°．

（1）如图15-1，若AO = OB，请写出AO与BD 的数量关系和位置关系；
（2）将图15-1中的MN绕点O顺时针旋转得到图15-2，其中AO = OB．
求证：AC = BD，AC ⊥ BD；
（3）将图15-2中的OB拉长为AO的k倍得到图15-3，求的值．

（本小题满分10分）

如图（1），在平面直角坐标系中，△OAB三个顶点坐标分别为O（0，0），A（1，），B（4，0）．

（1）求证：AB⊥OA

（2）在第一象限内确定点M，使△MOB与△AOB相似，求符合条件的点M的坐标．

（3）如图（2），已知D（0，-3），作直线BD．

     ①将△AOB沿射线BD平移4个单位长度后，求△AOB与以D为圆心，以1为半径的⊙D的公共点的个数．

②如图（3），现有一点P从D点出发，沿射线DB的方向以1个单位长度/秒的速度作匀速运动，运动时间为秒．当以P为圆心，以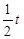为半径的⊙P与△AOB有公共点时，求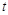的取值范围．

 

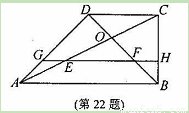
（本小题满分10分）在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，

对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F。

（1）求证：△FOE≌△DOC；

（2）求sin∠OEF的值；

（3）若直线EF与线段AD，BC分别相交于点G，H，求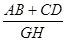的值。

 

 

（本小题满分10分）袋中装有除数字不同其它都相同的六个小球，球上分别标有数字1，2，3，4，5，6．
（1）从袋中摸出一个小球，求小球上数字小于3的概率；
（2）将标有1，2，3数字的小球取出放入另外一个袋中，分别从两袋中各摸出一个小球，求数字之和为偶数的概率．（要求用列表法或画树状图求解）