
题目列表(包括答案和解析)
集合的表示方法
(1)确定性:即集合中的元素必须是 的,任何一个对象都能明确判断它“是”或者“不是”某个集合的元素,二者必居其一且只居其一.?
(2)互异性:集合中任意两个元素都是 的.换言之,同一个元素在一个集合里不能重复出现.?
(3)无序性:集合与它的元素的组成方式是无关的.
对于复数![]() ,若集合
,若集合![]() 具有性质“对任意
具有性质“对任意![]() ,必有
,必有![]() ”,则当
”,则当 时,
时,![]() 等于
等于
A.1 B.-1 C.0 D.![]()
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合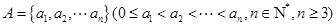 具有性质
具有性质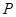 :对任意
:对任意 ,
,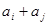 与
与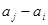 至少一个属于
至少一个属于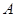 .
.
(1)分别判断集合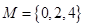 与
与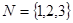 是否具有性质
是否具有性质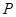 ,并说明理由;
,并说明理由;
(2)①求证: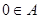 ;
;
②求证: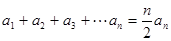 ;
;
(3)研究当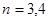 和
和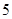 时,集合
时,集合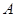 中的数列
中的数列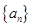 是否一定成等差数列.
是否一定成等差数列.
对于复数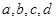 ,若集合
,若集合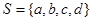 具有性质“对任意
具有性质“对任意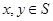 ,必有
,必有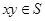 ”,则当
”,则当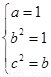 时,
时,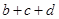 等于( )
等于( )
A.1 B.-1 C.0 D.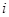
对于复数![]() ,若集合
,若集合![]() 具有性质“对任意
具有性质“对任意![]() ,必有
,必有![]() ”,则当
”,则当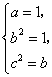 时,
时,![]() 等于
等于
A.1 B.-1 C.0 D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com