
题目列表(包括答案和解析)
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).

设f (x)=sin 2x+ (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 该函数的图象可由
 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(Ⅱ)若f (θ)= ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
【解析】第一问中,
即 变换分为三步,①把函数
变换分为三步,①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;
的图象;
第二问中因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而
进而得到结论。
(Ⅰ) 解:
即 。…………………………………3分
。…………………………………3分
变换的步骤是:
①把函数 的图象向右平移
的图象向右平移 ,得到函数
,得到函数 的图象;
的图象;
②令所得的图象上各点的纵坐标不变,把横坐标缩短到原来的 倍,得到函数
倍,得到函数 的图象;
的图象;
③令所得的图象上各点的横坐标不变,把纵坐标伸长到原来的2倍,得到函数 的图象;…………………………………3分
的图象;…………………………………3分
(Ⅱ) 解:因为 ,所以
,所以 ,则
,则 ,又
,又
 ,
, ,从而
,从而 ……2分
……2分
(1)当 时,
时, ;…………2分
;…………2分
(2)当 时;
时;
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当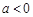 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com