
题目列表(包括答案和解析)
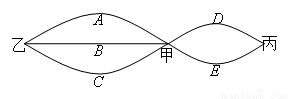
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情
况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机
的.同一条道路去程与回程是否堵车相互独立. 假设李生早上需要先开车送小孩去丙地小学,
再返回经甲地赶去乙地上班.假设道路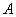 、
、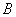 、
、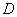 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是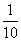 ,
,
道路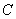 、
、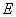 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是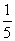 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
(1)求李生小孩按时到校的概率;
(2)李生是否有八成把握能够按时上班?
(3)设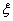 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求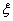 的均值.
的均值.
 .
.(本小题满分12分)
一项试验有两套方案,每套方案试验成功的概率都是 ,试验不成功的概率都是
,试验不成功的概率都是 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
(I)求3次试验都选择了同一套方案且都试验成功的概率:(II)记3次试验中,都选择了第一套方案并试难成功的次数为X,求X的分布列和期望EX.
按以下法则建立函数f(x):对于任何实数x,函数f(x)的值都是3-x与x2-4x+3中的最大者,则函数f(x)的最小值等于 .
(本小题满分13分)
现有甲、乙两个项目,对甲项目投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为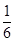 、
、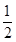 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是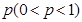 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为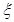 ,对乙项目投资十万元,
,对乙项目投资十万元, 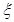 取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量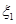 、
、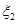 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求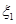 、
、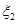 的概率分布和数学期望
的概率分布和数学期望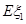 、
、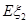 ;
;
(II)当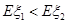 时,求
时,求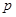 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com