(本题满分14分)已知函数f (x) = 的定义域集合是A，函数 g(x) = lg [x² ?? (2a + 1)x + a² + a]的定义域集合是B．（1）求集合A，B．（2）若AB = B，求实数a的取值范围．

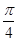(文科)(本题满分14分)设函数f(x)=·，其中=(m,cos2x)，=(1+sin2x,1)，x∈R，且函数y=f(x)的图象经过点(,2).

    (Ⅰ)求实数m的值；

    (Ⅱ)求函数f(x)的最小值及此时x值的集合

(理科)(本题满分14分)已知函数f(x)=e^x-kx，x∈R

    (Ⅰ)若k=e，试确定函数f(x)的单调区间

    (Ⅱ)若k>0，且对于任意x∈R，f(|x|)>0恒成立，试确定实数k的取值范围

．(本题满分14分)已知函数f(x)＝sin(ωx＋φ)，其中ω>0，|φ|<.

(1)若coscosφ－sinsinφ＝0，求φ的值；

(2)在(1)的条件下，若函数f(x)的图象的相邻两条对称轴之间的距离等于，求函数f(x)的解析式；并求最小正实数m，使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数．

(文科)(本题满分14分)设函数f(x)=·，其中=(m,cos2x)，=(1+sin2x,1)，x∈R，且函数y=f(x)的图象经过点(,2).
(Ⅰ)求实数m的值；
(Ⅱ)求函数f(x)的最小值及此时x值的集合
(理科)(本题满分14分)已知函数f(x)=e^x-kx，x∈R
(Ⅰ)若k=e，试确定函数f(x)的单调区间
(Ⅱ)若k>0，且对于任意x∈R，f(|x|)>0恒成立，试确定实数k的取值范围

(本题满分14分)已知函数f(x)满足2ax·f(x)=2f(x)-1,f(1)=1，设无穷数列{a_n}满足a_n+1=f(a_n).（1）求函数f(x)的表达式；（2）若a₁=3，从第几项起，数列{a_n}中的项满足a_n＜a_n+1；（3）若＜a₁＜（m为常数且m∈N+,m≠1），求最小自然数N，使得当n≥N时，总有0＜a_n＜1成立。