
题目列表(包括答案和解析)
如图一,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2.把△ABD沿BD折起(如图二),使二面角A-BD-C的余弦值等于![]() .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
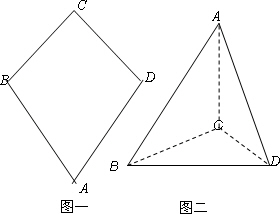
(1)求A,C两点间的距离;
(2)证明:AC⊥平面BCD;
(3)求直线AC与平面ABD所成角的正弦值.
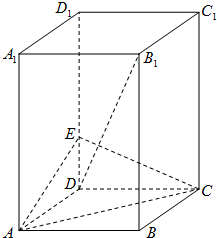 (2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点.
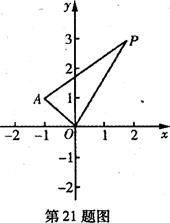
(2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点.(本小题满分1 2分)在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
(I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且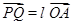 ,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
(本小题满分1 3分)
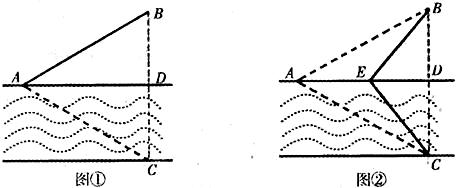
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤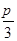 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
(本小题满分1 2分)
如图,四边形ABCD中,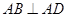 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD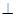 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
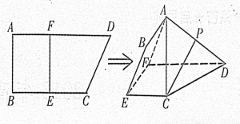
( I )当E为BC中点时,求证:CP//平面ABEF
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com