
题目列表(包括答案和解析)
(14分)已知函数![]() ,( x>0).
,( x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
(14分)一个袋中有8个大小相同的小球,其中红球1个,白球和黑球若干,现从袋中有放回地取球,每次随机取一个,又知连续取两次都是白球的概率为1/4.
(Ⅰ)求该口袋内白球和黑球的个数;
(Ⅱ)规定取出1个红球得2分,取出1个白色球得1分,取出1个黑色球得0分,连续取三次分数之和为4分的概率;
(Ⅲ)现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取,乙后取,然后甲在取,直到两个小朋友中有1人取得黑球时游戏终止,每个球在每一次被取出的机会均相同,求当游戏终止时,取球次数不多于3次的概率.
(本题14分)已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?
为邻边的平行四边形是菱形?
 若存在,求出
若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本题14分)已知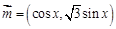 ,
,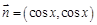 ,设
,设 .
.
(1)求函数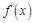 的图像的对称轴及其单调递增区间;
的图像的对称轴及其单调递增区间;
(2)当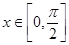 ,求函数
,求函数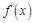 的值域及取得最大值时
的值域及取得最大值时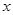 的值;
的值;
(3)若 分别是锐角
分别是锐角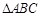 的内角
的内角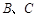 的对边,且
的对边,且 ,
,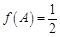 ,试求
,试求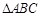 的面积
的面积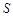 .
.
(本题14分)北京奥运会纪念章某特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元.
元.
(Ⅰ)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式(并写出这个函数的定义域);
的函数关系式(并写出这个函数的定义域);
(Ⅱ)当每枚纪念销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值.
(元)最大,并求出这个最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com