
题目列表(包括答案和解析)
如图是函数f(x)=Asinωx(A>0,ω>0)一个周期的图象,则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值等于
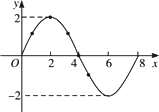
![]()
![]()
2+![]()
2![]()
| x+sinx |
| x |
| x-3 |
| 4-x |
已知函数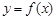 是
是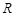 上的偶函数,对于
上的偶函数,对于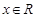 都有
都有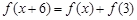 成立,且
成立,且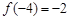 ,当
,当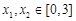 且
且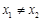 时,都有
时,都有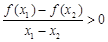 ,则给出下列命题:
,则给出下列命题:
①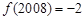 ;②函数
;②函数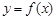 图象的一条对称轴为
图象的一条对称轴为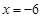 ;③函数
;③函数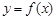 在
在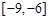 上为减函数;④
方程
上为减函数;④
方程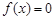 在
在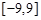 上有4个根 ,上述命题中的所有正确命题的序号是 .(把你认为正确命题的序号都填上)
上有4个根 ,上述命题中的所有正确命题的序号是 .(把你认为正确命题的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com