同学们学习了《必修1》的函数一章，初步掌握了研究函数的一些基本方法。在下面的学习中我们将接触三角函数，比如我们要学习“正弦三角函数y=sinx”,请你谈谈你想从那几个方面来研究这个函数。（可类比研究指数函数与对数函数的方法，至少说出4个方面）

1、­­                           

 

2、                           

 

3、                           

 

4、                           

我们知道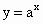，(0＜a≠1)与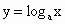(0＜a≠1)互为反函数，只要把同底的指数函数与对数函数的解析式互化，就可以由其中的一个得到它的反函数的解析式．仿此，请探究函数y=2x＋1是否有反函数．如果有，你能否求出反函数？

我们知道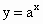，(0＜a≠1)与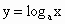(0＜a≠1)互为反函数，只要把同底的指数函数与对数函数的解析式互化，就可以由其中的一个得到它的反函数的解析式．仿此，请探究函数y=2x＋1是否有反函数．如果有，你能否求出反函数？

(1)对数的概念:如果a^b=N(a＞0,a≠1),那么幂指数b叫做以a为底数N的对数，记作　　　　　，其中a叫做底数，N叫做　　　　　.?

(2)积、商、幂、方根的对数(M，N都是正数，a＞0，且a≠1,n≠0).?

①=　　　　　;?

② =　　　　　;?

③ =　　　　　;?

(3)对数的换底公式及对数恒等式(供选用).?

① =　　　　　(对数恒等式);?

② =　　　　　;?

③ (换底公式);?

④;?

⑤.?

(4)指数式与对数式的关系如下表:

 

	式子	名称
		a	b	N
指数式	ab=N
对数式	logaN=b

 

关于x的方程x+2^x=2，x+log₂x=2的解分别为α、β，根据指数函数和对数函数的图象，α+β=．