
题目列表(包括答案和解析)
已知函数 在
在 处取得极值2.
处取得极值2.
⑴ 求函数 的解析式;
的解析式;
⑵ 若函数 在区间
在区间 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
【解析】第一问中利用导数
又f(x)在x=1处取得极值2,所以 ,
,
所以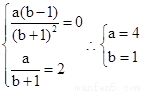
第二问中,
因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得
解:⑴ 求导 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以 ,即
,即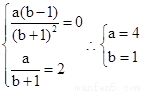 ,所以
,所以 …………6分
…………6分
⑵ 因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得 , …………9分
, …………9分
当f(x)在区间(m,2m+1)上单调递减,则有
得 …………12分
…………12分
.综上所述,当 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是 或
或
 ,当x每增加一个单位时,
,当x每增加一个单位时, 平均增加12个单位;
平均增加12个单位; |
| y |
 |
| y |
下列说法正确的是 。
(1)从匀速传递的产品生产流水线上,质检人员每20分钟从中抽取一件产品进行检测,这样的抽样方法为分层抽样;
(2)两个随机变量相关性越强,相关系数 的绝对值越接近1,若
的绝对值越接近1,若 或
或 时,则
时,则 与
与 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
(3)在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)对于回归直线方程 ,当
,当 每增加一个单位时,
每增加一个单位时, 平均增加12个单位;
平均增加12个单位;
(5)已知随机变量 服从正态分布
服从正态分布
 ,若
,若 ,则
,则 。
。
下列说法正确的是 。
(1)从匀速传递的产品生产流水线上,质检人员每20分钟从中抽取一件产品进行检测,这样的抽样方法为分层抽样;
(2)两个随机变量相关性越强,相关系数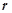 的绝对值越接近1,若
的绝对值越接近1,若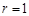 或
或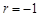 时,则
时,则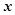 与
与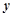 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
(3)在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)对于回归直线方程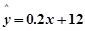 ,当
,当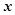 每增加一个单位时,
每增加一个单位时,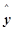 平均增加12个单位;
平均增加12个单位;
(5)已知随机变量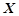 服从正态分布
服从正态分布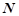
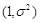 ,若
,若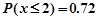 ,则
,则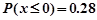 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com