题目列表(包括答案和解析)
(1)我们规定正数的正分数指数幂的意义是：
________＝(a＞0，m、n∈N*，n＞1)；
(2)正数的负分数指数幂的意义与负整数指数幂的意义相仿：我们规定＝________(a＞0，m、n∈N*且n＞1)．
整数指数幂的运算性质对于有理指数幂也同样适用，即对于任意有理数
r，s，均有下面的运算性质：
你能利用根式与分数指数幂的知识证明上述的运算性质吗？
整数指数幂的运算性质对于有理指数幂也同样适用，即对于任意有理数r，s，均有下面的运算性质：
你能利用根式与分数指数幂的知识证明上述的运算性质吗？
证明整数指数幂的运算性质
(1)：
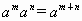．有理指数幂的运算性质：
(1)ar·as＝________；
(2)(ar)s＝________；
(3)(ab)r＝________．(a＞0，b＞0，r、s∈Q)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com