
题目列表(包括答案和解析)
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA?

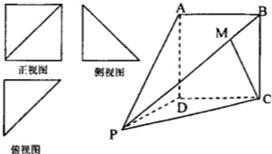 一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图. 一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.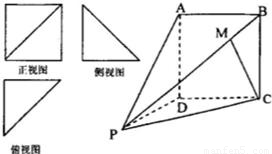
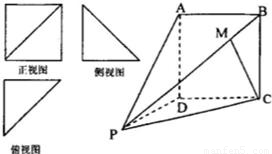
一.选择题
D A C C C A A C D B
二.填空题
11.32 12. 6 13. .files/image246.gif) 14. 10 ,0.8 15.
14. 10 ,0.8 15. .files/image248.gif) 或
或.files/image250.gif) 16.3,-1
16.3,-1
17. .files/image252.gif)
三.解答题
18.解:(1).files/image254.gif)
.files/image256.gif)
.files/image258.gif)
而.files/image260.gif) 是极值点,所以
是极值点,所以.files/image262.gif) 解之得:
解之得:.files/image264.gif)
又.files/image266.gif) ,故得
,故得.files/image268.gif)
(2)由(1)可知.files/image270.gif) 而
而.files/image202.gif) 是它的极小值点,所以函数
是它的极小值点,所以函数.files/image218.gif) 的极小值为-25.
的极小值为-25.
19.解:,显然ξ所有可能取的值为0,1,2,3
P(ξ=0)=.files/image274.gif) ,P(ξ=1)=
,P(ξ=1)=.files/image276.gif) P(ξ=2)=
P(ξ=2)=.files/image278.gif)
P(ξ=3)=.files/image280.gif)
Eξ=.files/image282.gif)
20.解(1)如图,以D为坐标原点,分别以.files/image284.gif) 所在直线为
所在直线为
.files/image286.gif)
点为E,则.files/image288.gif) 是平面PBC的法向量;设AP中点为F,同理
是平面PBC的法向量;设AP中点为F,同理
可知.files/image290.gif) 是平面PAB的法向量。知
是平面PAB的法向量。知.files/image290.gif) 是平面
是平面.files/image293.gif) 的法向量。
的法向量。.files/image295.gif) ,
,
设二面角.files/image297.gif) ,显然
,显然.files/image299.gif) 所以
所以
.files/image301.jpg) 二面角
二面角.files/image303.gif) 大小为
大小为.files/image305.gif) ;…
;…
(2)P(2,0,0),B(0,2,2),C(0,2,0),A(0,0,2),.files/image307.gif) 共线,
共线,.files/image309.gif) 可设
可设.files/image311.gif)
.files/image313.gif)
.files/image315.gif)
.files/image317.gif)
.files/image319.gif) 的长为
的长为.files/image243.gif) 时,
时,.files/image322.gif)
21.解:(1).files/image324.gif) 依题意,知方程
依题意,知方程.files/image326.gif) 有实根,所以
有实根,所以.files/image328.gif) 得
得.files/image330.gif)
(2)由函数.files/image218.gif) 在
在.files/image223.gif) 处取得极值,知
处取得极值,知.files/image223.gif) 是方程
是方程.files/image326.gif) 的一个根,所以
的一个根,所以.files/image332.gif) , 方程
, 方程.files/image326.gif) 的另一个根为
的另一个根为.files/image334.gif) 因此,当
因此,当.files/image336.gif) ,当
,当.files/image338.gif) 所以,
所以,.files/image340.gif) 和
和.files/image342.gif) 上为增函数,在
上为增函数,在.files/image344.gif) 上为减函数,
上为减函数,.files/image346.gif) 有极大值
有极大值.files/image348.gif) ,
,
又.files/image350.gif)
.files/image352.gif)
.files/image354.gif) 恒成立,
恒成立,.files/image356.gif)
.files/image358.gif)
四.附加题
22.解:由.files/image360.gif)
(1)①当.files/image362.gif) 不存在极值
不存在极值
②当.files/image364.gif) 恒成立
恒成立
.files/image366.gif) 不存在极值a的范围为
不存在极值a的范围为.files/image368.gif)
.files/image366.gif) 存在极值a的范围为
存在极值a的范围为.files/image370.gif)
(2)由.files/image372.gif) 恒成立
恒成立
①当.files/image374.gif) 恒成立 ∴a=0,
恒成立 ∴a=0,
②当.files/image376.gif)
.files/image378.gif) ③当
③当.files/image380.gif)
1.若.files/image382.gif)
.files/image384.gif)
2.若.files/image386.gif) 为单减函数
为单减函数
.files/image388.gif)
综上:①②③得:.files/image390.gif) 上为增函数,
上为增函数, .files/image392.gif)
23.解法一:(1)方法一:作.files/image394.gif) 面
面.files/image396.gif) 于
于.files/image398.gif) ,连
,连.files/image400.gif) .
.
.files/image402.gif)
.files/image404.gif) .
.
.files/image406.gif) .
.
又.files/image408.gif) ,则
,则.files/image410.gif) 是正方形.
是正方形.
则.files/image412.gif) .
.
方法二:取.files/image414.gif) 的中点
的中点.files/image416.gif) ,连
,连.files/image418.gif) ,
,
则有.files/image420.gif) .
.
.files/image422.gif) 面
面.files/image424.gif) ,
,.files/image426.gif) .
.
.files/image427.gif) (2)作
(2)作.files/image429.gif) 于
于.files/image431.gif) ,作
,作.files/image433.gif) 交
交.files/image435.gif) 于
于.files/image437.gif) ,
,
则.files/image439.gif) 就是二面角
就是二面角.files/image441.gif) 的平面角.
的平面角.
.files/image443.gif) ,
,
.files/image445.gif) 是
是.files/image447.gif) 的中点,且
的中点,且.files/image449.gif) .
.
则.files/image451.gif) .
.
由余弦定理得.files/image453.gif) ,
,
.files/image455.gif) .
.
(3)设.files/image457.gif) 为所求的点,作
为所求的点,作.files/image459.gif) 于
于.files/image461.gif) ,连
,连.files/image463.gif) .
.
则.files/image465.gif) ,
,
.files/image467.gif) 面
面.files/image469.gif) 就是
就是.files/image471.gif) 与面
与面.files/image396.gif) 所成的角,则
所成的角,则.files/image473.gif) .
.
设.files/image475.gif) ,易得
,易得.files/image477.gif) ,则
,则.files/image479.gif) ,
,.files/image481.gif) .
.
.files/image483.gif) ,解得
,解得.files/image485.gif) ,则
,则.files/image487.gif) .
.
故线段.files/image447.gif) 上存在
上存在.files/image457.gif) 点,且
点,且.files/image491.gif) 时,
时,.files/image471.gif) 与面
与面.files/image396.gif) 成
成.files/image493.gif) 角.
角.
解法二:
(1)作.files/image394.gif) 面
面.files/image396.gif) 于
于.files/image398.gif) ,连
,连.files/image497.gif) ,则四边形
,则四边形.files/image410.gif) 是正方形,且
是正方形,且.files/image500.gif) ,
,
.files/image501.gif) 以
以.files/image503.gif) 为原点,以
为原点,以.files/image505.gif) 为
为.files/image048.gif) 轴,
轴,.files/image508.gif) 为
为.files/image510.gif) 轴建立空间直角坐标系如图,
轴建立空间直角坐标系如图,
则.files/image512.gif) .
.
.files/image514.gif) ,
,
.files/image516.gif) ,则
,则.files/image518.gif) .
.
(2)设平面.files/image520.gif) 的法向量为
的法向量为.files/image522.gif) ,
,
则由.files/image524.gif) 知:
知:.files/image526.gif) ;
;
同理由.files/image528.gif) 知:
知:.files/image530.gif) .
.
可取.files/image532.gif) .
.
同理,可求得平面.files/image534.gif) 的一个法向量为
的一个法向量为.files/image536.gif) .
.
由图可以看出,二面角.files/image441.gif) 的大小应等于
的大小应等于.files/image539.gif)
则.files/image541.gif) ,即所求二面角的大小是
,即所求二面角的大小是.files/image543.gif) .
.
(3)设.files/image545.gif) 是线段
是线段.files/image447.gif) 上一点,则
上一点,则.files/image547.gif) ,
,
平面.files/image396.gif) 的一个法向量为
的一个法向量为.files/image550.gif) ,
,.files/image552.gif) ,
,
要使.files/image471.gif) 与面
与面.files/image396.gif) 成
成.files/image493.gif) 角,由图可知
角,由图可知.files/image557.gif) 与
与.files/image559.gif) 的夹角为
的夹角为.files/image561.gif) ,
,
所以.files/image563.gif) .
.
则.files/image565.gif) ,解得,
,解得,.files/image485.gif) ,则
,则.files/image487.gif) .
.
故线段.files/image447.gif) 上存在
上存在.files/image457.gif) 点,且
点,且.files/image491.gif) 时,
时,.files/image471.gif) 与面
与面.files/image396.gif) 成
成.files/image493.gif) 角.
角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com