（14分）

（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即，k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式。已知引力常量为G，太阳的质量为M_太。

（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测定月地距离为3.84×10⁸m，月球绕地球运动的周期为2.36×10⁶S，试计算地球的质M_地。（G=6.67×10^-11Nm²/kg²，结果保留一位有效数字）

【解析】：（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有

                            ①

    于是有                           ②

即                                ③

（2）在月地系统中，设月球绕地球运动的轨道半径为R，周期为T，由②式可得

                                ④

解得     M_地=6×10²⁴kg                         ⑤

（M_地=5×10²⁴kg也算对）

23．【题文】（16分）

     如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t₀时间从P点射出。

（1）求电场强度的大小和方向。

（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。

（3）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。

在物理学上，常利用测定带电粒子的受力情况来确定复合场中场强的大小和方向。如图所示，在立方体区域内存在待测定的匀强电场和匀强磁场，在其左侧分别是加速电场和速度选择器，用于获取特定速度的带电粒子。装置中，灯丝A接入电源后发出电子，P为中央带小圆孔的竖直金属板，在灯丝A和金属板P之间接入电源甲，使电子加速；在间距为d的水平正对金属板C、D间接入电源乙，在板间形成匀强电场。C、D间同时存在垂直纸面向外、大小为 B0的匀强磁场（左右宽度与两板相同）。现将电源甲、乙的输出电压分别调到U₁、U₂，使电子沿直线运动进入待测区域，如图中虚线所示。电子质量为m、电量为e，重力不计，从灯丝出来的电子初速不计，整个装置置于真空室内。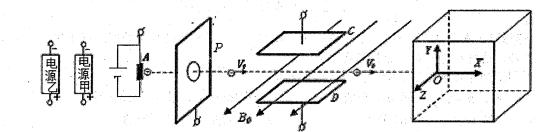

（1）用笔画线代替导线将电源甲、乙接人装置，以满足题中要求；
（2）求电子从P板出来的速度v₀及U₁、U₂。满足的关系式；
（3）调节U₁、U₂使电子以不同的速度大小沿+X轴进入待测区域，测得电子刚连入时受力大小均为F，由此，你能推测出待测区域中电场或磁场的什么信息？
（4）保持电子进入待测区域的速度大小仍为V₀，转动待测区域（转动中电场、磁场相对坐标轴的方向不变），使电子沿Y轴或Z轴方向射入。测得电子刚射入时受力大小如下表所示，根据表中信息又能推测出待测区域中电场或磁场的什么信息？

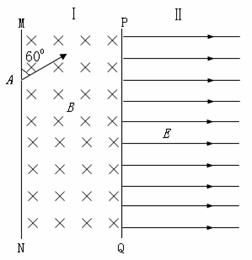
如图所示，在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场，其边界为MN、PQ，其中PQ边界位置可以左右调节。在PQ右边空间区域Ⅱ存在水平向右的匀强电场，其范围足够宽。在左边界的A点处有一个质量为m=1.0×10^-12kg、带电量大小为q=1.0×10^-13C的负电粒子，以速度V₀=3m/s沿着与左边界成60°的方向射入磁场，粒子重力不计，求：

（1）粒子在磁场中做圆周运动的半径

（2）若带电粒子从边界PQ飞出磁场，进入电场，经过一段时间，运动到电场中的C点，速度刚好减为零。求满足此种运动情况的磁场宽度以及粒子从A点到C点的时间；

（3）调节磁场与电场分界线PQ的位置，使粒子在磁场中运动的时间为,恰好到达边界PQ时撤去磁场，同时将电场反向，粒子进入电场，经过一段时间到达D点，此时粒子速度方向与进入磁场时A点处的速度方向垂直，求粒子磁场中做圆周运动的圆心O点到D点的距离S。（结论可保留成根号形式）