
题目列表(包括答案和解析)
(本题16分) 本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
.
(本题满分16分)定义在 的函数
的函数
(1)对任意的 都有
都有 ;
;
(2)当 时,
时, ,回答下列问题:
,回答下列问题:
①判断 在
在 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②判断 在
在 的单调性,并说明理由;
的单调性,并说明理由;
③若 ,求
,求 的值.
的值.
(本小题满分16分)设数列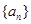 的前n项和为
的前n项和为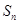 ,数列
,数列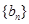 满足:
满足: 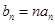 ,且数列
,且数列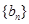 的前
的前
n项和为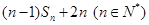 .
.
(1) 求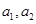 的值;
的值;
(2) 求证:数列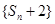 是等比数列;
是等比数列;
(3) 抽去数列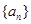 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列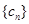 ,若
,若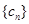 的前n项和为
的前n项和为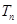 ,求证:
,求证: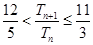 .
.
(本题满分16分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .数列
.数列![]() 中,
中,![]() ,
,
![]()
![]() .(1)求数列
.(1)求数列![]() 的通项公式;(2)若存在常数
的通项公式;(2)若存在常数![]() 使数列
使数列![]() 是等比数列,求数列
是等比数列,求数列![]() 的通项公式;(3)求证:①
的通项公式;(3)求证:①![]() ;②
;②![]() .
.
(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为 元,则他的满意度为
元,则他的满意度为 ;如果他买进该产品的单价为
;如果他买进该产品的单价为 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和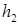 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为 元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1)求 和
和 关于
关于 、
、 的表达式;当
的表达式;当 时,求证:
时,求证: =
= ;
;
(2)设 ,当
,当 、
、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为 ,试问能否适当选取
,试问能否适当选取 、
、 的值,使得
的值,使得 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com