
题目列表(包括答案和解析)
(本小题满分14分)
某工厂生产一种产品的成本费共由三部分组成:①原材料费每件50元;②职工工资支出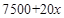 元;③电力与机器保养等费用为
元;③电力与机器保养等费用为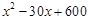 元.其中
元.其中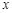 是该厂生产这种产品的总件数。
是该厂生产这种产品的总件数。
(1)把每件产品的成本费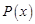 (元)表示成产品件数
(元)表示成产品件数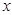 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量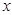 不超过170件且能全部销售,根据市场调查,每件产品的销售价为
不超过170件且能全部销售,根据市场调查,每件产品的销售价为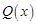 (元),且
(元),且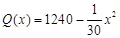 ,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
(本题满分14分
某工厂生产一种产品的成本费由三部分组成
①职工工资固定支出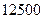 元
元
②原材料费每件40元
③电力与机器保养等费用为每件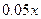 元,其中
元,其中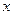 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费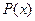 (元)表示成产品件数
(元)表示成产品件数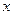 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量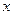 不超过
不超过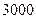 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价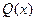 与产品件数
与产品件数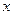 有如下关系:
有如下关系: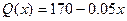 ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
(本题满分14分
某工厂生产一种产品的成本费由三部分组成
①
职工工资固定支出 元
元
② 原材料费每件40元
③
电力与机器保养等费用为每件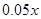 元,其中
元,其中 是该厂生产这种产品的总件数.
是该厂生产这种产品的总件数.
(1)把每件产品的成本费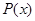 (元)表示成产品件数
(元)表示成产品件数 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量 不超过
不超过 件,且产品能全部销售.根据市场调查:每件产品的销售价
件,且产品能全部销售.根据市场调查:每件产品的销售价 与产品件数
与产品件数 有如下关系:
有如下关系: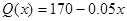 ,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
,试问生产多少件产品,总利润最高?(总利润=总销售额—总的成本)
(本小题满分14分)
设![]() ,
,![]() 是平面直角坐标系
是平面直角坐标系![]() 上的两点,现定义由点
上的两点,现定义由点![]() 到点
到点![]() 的一种折线距离
的一种折线距离![]() 为
为
![]()
对于平面![]() 上给定的不同的两点
上给定的不同的两点![]() ,
,![]() ,
,
(1)若点![]() 是平面
是平面![]() 上的点,试证明
上的点,试证明![]()
(2)在平面![]() 上是否存在点
上是否存在点![]() ,同时满足
,同时满足
①![]() ②
② ![]()
若存在,请求出所有符合条件的点,请予以证明。
(09年湖北黄冈联考理)(14分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() ”
”
(1)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)若集合M中的元素具有下面的性质:“若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立”
成立”
试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(3)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中的任意的
定义域中的任意的![]() ,当
,当![]() 且
且![]() 时,
时,![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com