
题目列表(包括答案和解析)
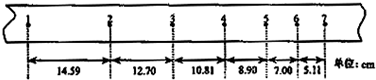
|
|
|
|
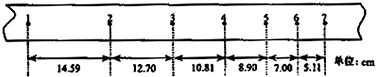
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
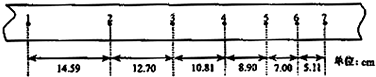
|
(2)为了测量一个高楼的高度,某同学设计了如下实验:在一根长为![]() 的绳两端各拴一重球,一人站在楼顶上,手执上端的重球无初速度的释放使其自由下落,另一人在楼下测量两球落地的时间差
的绳两端各拴一重球,一人站在楼顶上,手执上端的重球无初速度的释放使其自由下落,另一人在楼下测量两球落地的时间差![]() ,即可根据
,即可根据![]() 、
、![]() 、
、![]() 得出高楼的高度(不计空气阻力).
得出高楼的高度(不计空气阻力).
①从原理上讲,这个方案是否正确_____________,理由:_________________.
②从实际测量来看,你估计最大的困难是__________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com