巳知二次函数y＝a(x²－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．

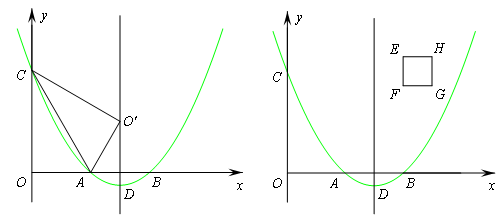
（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；

（2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；

（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．

【解析】二次函数的综合运用

巳知二次函数y＝a(x²－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．

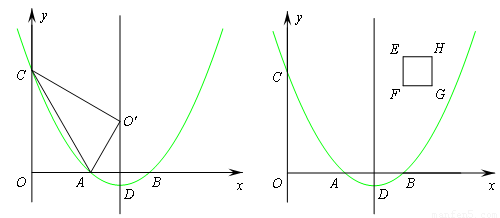
（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；

（2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；

（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．

【解析】二次函数的综合运用

将直线y=2x-3向右平移3个单位，再向上平移1个单位，求平移后的直线的关系式．
解：在直线y=2x-3上任取两点A（1，-1），B（0，-3）．
由题意知：
点A向右平移3个单位得A′（4，-1）；再向上平移1个单位得A″（4，0）
点B向右平移3个单位得B′（3，-3）；再向上平移1个单位得B″（3，-2）
设平移后的直线的关系式为y=kx+b．
则点A″（4，0），B″（3，-2）在该直线上，
可解得k=2，b=-8．
所以平移后的直线的关系式为y=2x-8．
根据以上信息解答下面问题：
将二次函数y=-x²+2x+3的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的关系式．（平移抛物线形状不变）