如图，用A、B、C三类不同的无件连接成两个系统N₁、N₂，当元件A、B、C都正常工作时，系统N₁正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N₂正常工作．已知元件A、B、C正常工作的概率依次为0.80，0.90，0.90；分别求系统N₁、N₂正常工作的概率P₁、P₂。

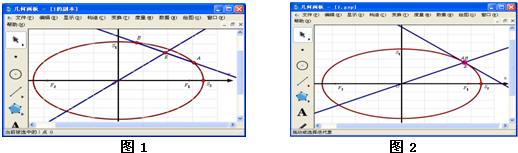
某同学用《几何画板》研究椭圆的性质：打开《几何画板》软件，绘制某椭圆C₁：

x2

a2

+

y2

b2

=1，在椭圆上任意画一个点S，度量点S的坐标（x_s，y_s），如图1．
（1）拖动点S，发现当x_s=

2

时，y_s=0；当x_s=0时，y_s=1，试求椭圆C₁的方程；
（2）该同学知圆具有性质：若E为圆O：x²+y²=r²（r＞0）的弦AB的中点，则直线AB的斜率k_AB与直线OE的斜率k_OE的乘积k_AB•k_OE为定值．该同学在椭圆上构造两个不同的点A、B，并构造直线AB，再构造AB的中点E，经观察得：沿着椭圆C₁，无论怎样拖动点A、B，椭圆也具有此性质．类比圆的这个性质，请写出椭圆C₁的类似性质，并加以证明；
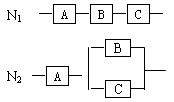
（3）拖动点A、B的过程中，如图2发现当点A与点B在C₁在第一象限中的同一点时，直线AB刚好为C₁的切线l，若l分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值．