
题目列表(包括答案和解析)
(本题满分13分)
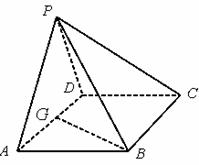
如图,在四棱锥![]() 中,底面
中,底面![]() 是
是![]() 且边长为
且边长为![]() 的菱形,侧面
的菱形,侧面![]() 是等边三角形,且平面
是等边三角形,且平面![]() 垂直于底面
垂直于底面![]() .
.
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求二面角![]() 的大小.
的大小.
(本题满分13分)
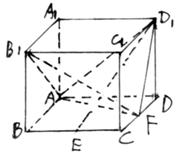
如图在棱长为2的正方体![]() 中,点F为棱CD中点,点E在棱BC上
中,点F为棱CD中点,点E在棱BC上
(1)确定点E位置使![]() 面
面![]() ;
;
(2)当![]() 面
面![]() 时,求二面角
时,求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
 (本小题满分13分)已知正四棱锥P—ABCD的高为
(本小题满分13分)已知正四棱锥P—ABCD的高为![]() ,底面边长为
,底面边长为![]() ,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为
,其内接正四棱柱EFGH—E1F1G1H1的四个顶点E、F、G、H在底面上,另外四个顶点E1、F1、G1、H1分别在棱PA、PB、PC、PD上(如图所示),设正四棱柱的底面边长为![]() .
.
(Ⅰ)设内接正四棱柱的体积为![]() ,求出函数
,求出函数![]() 的解析式;
的解析式;
(Ⅱ)试求该内接正四棱柱的最大体积及对应的![]() 的值.
的值.
(本小题满分13分)
如图,在三棱柱 中,
中, 是正方形
是正方形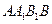 的中心,
的中心,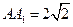 ,
,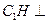 平面
平面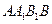 ,且
,且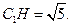
(Ⅰ)求异面直线与所成角的余弦值;
(Ⅱ )求二面角
)求二面角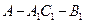 的正弦值;
的正弦值;
(Ⅲ)设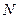 为棱
为棱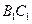 的中点,点
的中点,点 在平面
在平面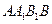 内,且
内,且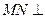 平面
平面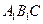 ,求线段
,求线段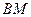 的长.
的长.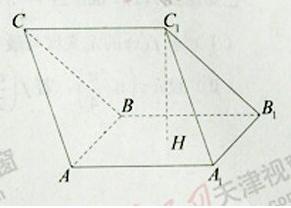
(本小题满分13分)如图所示,四棱锥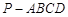 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱 上的动点.
上的动点.
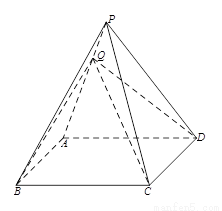
(Ⅰ)若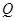 是
是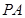 的中点,求证:
的中点,求证: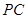 //平面
//平面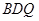 ;
;
(Ⅱ)若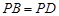 ,求证:
,求证: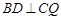 ;
;
(III)在(Ⅱ)的条件下,若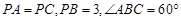 ,求四棱锥
,求四棱锥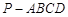 的体积.
的体积.
一、选择题:本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个是符合题目要求的。
1―8 BDABADBC
二、填空题:本大题共有6个小题,每小题5分,共30分;请把答案写在相应的位置上。
9.5 10. 11.7 12.
11.7 12. 13.
13. 14.
14.
三、解答题:本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤。
15.(本题满分13分)
解:(1)

(2)

16.(本题满分13分)
解: 用A,B,C分别表示事件甲、乙、丙面试合格.
由题意知A,B,C相互独立,且
P(A)=P(B)=P(C)= .
.
(Ⅰ)至少有1人面试合格的概率是
 …………………6分
…………………6分
(2)没有人签约的概率为

 ………………13分
………………13分
17.(本题满分13分)
解法1:(1)连结A1B,则D1E在侧面ABB
又∵A1B⊥AB1,
|