查看答案和解析>>

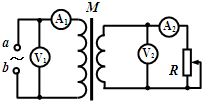B．如图所示，M为理想变压器，电表均视为理想电表，输入端a、b接正弦交流电源时，原线圈中电压表和电流表的示数分别为U₁和I₁，副线圈中电压表和电流表的示数分别为U₂和I₂，则原线圈与副线圈的匝数之比等于

 

；当滑动变阻器的滑片P向上滑动时，示数发生变化的电表是

 

．

查看答案和解析>>

B． 滑雪者从A点由静止沿斜面滑下，沿一平台滑过后水平飞离B点，最后落到地面，空间几何尺度（H、h和L）如图所示．斜面、平台与滑雪板之间的动摩擦因数为μ．假设滑雪者由斜面底端进入平台后立即沿水平方向运动，且速度大小不变．求：
（1）滑雪者从A到B的过程中，克服摩擦力做的功；
（2）滑雪者离开B点时的速度大小；
（3）滑雪者从B点开始做平抛运动，到达地面时的速度大小．

查看答案和解析>>

B．如图所示，一个半径为R=0.45m的光滑半圆柱面固定在水平面上，在圆柱的最高点有一个小物体，以垂直于圆柱的方向、大小为υ₀=1.2m/s的水平初速度离开最高点．求：小物体落地的位置？
某同学的解答过程是：
小物体落地的时间 t=

2h/g

=

2x0.45/10

s=0.3s
小物体落地点离圆柱面的距离 s=υt=1.2m/s×0.3s=0.36m
你认为该同学的解答过程是否正确？请你说明理由，如果你认为不正确，也请说明理由．

查看答案和解析>>

B．一横波某瞬时波形如图所示，质点M此时的运动方向向下，且经过0.2s第一次回到平衡位置，则此横波的波长为

6

6

cm，传播方向是向

左

左

，波速为

5

5

cm/s，从图示时刻起，经过1.2s，质点M通过的路程为

8

8

cm．

查看答案和解析>>

一、1、C 2、D 3、BD 4、A 5、ABD 6、B7、A 8、A

9、AC 10、C 11、AC  12、AC

二、实验题（本题共2小题共18分）将答案填在横线上或作图和连线.

13、（8分）2   （4分）   B（4分）

14、（10分）I．对于甲图不合理之处；②不能多次测量，

②超过电流表量程，不安全，③电压表

量程太大，读数误差较大。             （3分）

II．对于乙图不合理之处：①电流表量程太小，

②电压表量程太大，③电压调节范围太小。      （3分）

Ⅲ．较为合理的电路图如图所示。R_x的计算公式：   （2分）

其中U_A是电压表V₁示数，I_A是电流表A₁示数，R_0­是电阻箱示数。  （2分）

三、本大题共四小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

15、（12分）（1）设绝缘板A匀加速和匀减速运动过程中的加速度大小分别为a₁和a₂，由绝缘板A运动的速度随时间变化的图象2可知，加速运动的时间t₁=0.8s，减速运动的时间为t₂=0.2s，

所以：  （4分）

（2）以滑块B为研究对象：

分析：当板A做匀加速运动时，滑块B处于超重状态，滑块B不会相对于A板滑动，当板A做匀减速运动时，滑块B处于失重状态而滑动，设滑块B在水平方向的加速度为a₃，

受力分析如图1所示：