查看答案和解析>>

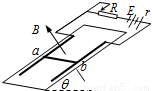
如图所示，在倾角θ=37°的斜面上，固定着宽L=0.20m的平行金属导轨，在导轨上端接有电源和滑动变阻器，已知电源电动势E=6.0V，内电阻r=0.50Ω．一根质量m=10g的金属棒ab放在导轨上，与两导轨垂直并接触良好，导轨和金属棒的电阻忽略不计．整个装置处于磁感应强度B=0.50T、垂直于轨道平面向上的匀强磁场中．若金属导轨是光滑的，已知sin37°=0.6，cos37°=0.8，取g=10m/s²，求：
（1）要保持金属棒静止在导轨上，滑动变阻器接入电路的阻值是多大？
（2）金属棒静止在导轨上时，如果使匀强磁场的方向瞬间变为竖直向上，则此时导体棒的加速度是多大？

查看答案和解析>>

如图所示，在倾角α=37°的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一质量m=3kg，中间有一圈凹槽的圆柱体，并用与斜面夹角β=37°的力F拉住，使整个装置处于静止状态．不计一切摩擦，求拉力F和斜面对圆柱体的弹力N的大小． （g=10m/s²，sin37°=0.6，cos37°=0.8）

查看答案和解析>>

如图所示，在倾角α=37°的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一质量m=3kg，中间有一圈凹槽的圆柱体，并用与斜面夹角β=37°的力F拉住，使整个装置处于静止状态．不计一切摩擦，求拉力F和斜面对圆柱体的弹力N的大小． （g=10m/s²，sin37°=0.6，cos37°=0.8）

查看答案和解析>>

如图所示，在倾角θ=37°的足够长的固定斜面上，有一质量m=1kg的物体，物体与斜面间动摩擦因数μ=0.2．物体受到沿平行于斜面向上的轻细线的拉力F=9.6N的作用，从静止开始运动，经2s绳子突然断了．求绳断后多长时间物体速度大小为22m/s．（结果保留两位有效数字，已知sin37°=0.6，g取10m/s²）

查看答案和解析>>

一、1、C 2、D 3、BD 4、A 5、ABD 6、B7、A 8、A

9、AC 10、C 11、AC  12、AC

二、实验题（本题共2小题共18分）将答案填在横线上或作图和连线.

13、（8分）2   （4分）   B（4分）

14、（10分）I．对于甲图不合理之处；②不能多次测量，

②超过电流表量程，不安全，③电压表

量程太大，读数误差较大。             （3分）

II．对于乙图不合理之处：①电流表量程太小，

②电压表量程太大，③电压调节范围太小。      （3分）

Ⅲ．较为合理的电路图如图所示。R_x的计算公式：   （2分）

其中U_A是电压表V₁示数，I_A是电流表A₁示数，R_0­是电阻箱示数。  （2分）

三、本大题共四小题共计54分．解答时请写出必要的文字说明、方程式和重要的演算步骤．只写出最后答案的不能得分．有数值计算的题．答案中必须明确写出数值和单位

15、（12分）（1）设绝缘板A匀加速和匀减速运动过程中的加速度大小分别为a₁和a₂，由绝缘板A运动的速度随时间变化的图象2可知，加速运动的时间t₁=0.8s，减速运动的时间为t₂=0.2s，

所以：  （4分）

（2）以滑块B为研究对象：

分析：当板A做匀加速运动时，滑块B处于超重状态，滑块B不会相对于A板滑动，当板A做匀减速运动时，滑块B处于失重状态而滑动，设滑块B在水平方向的加速度为a₃，

受力分析如图1所示：