练习册

  • 练习册
  • 试题
    (A)∥平面.且到平面的距离为 【查看更多】

     

    题目列表(包括答案和解析)

    平面直角坐标系xOy中，动点P从点P0（4，0）出发，运动过程中，到定点F（-2，0）的距离与到定直线l：x=-8的距离之比为常数．
    ①求点P的轨迹方程；
    ②在轨迹上是否存在点M（s，t），使得以M为圆心且经过定点F（-2，0）的圆与直线x=8相交于两点A、B？若存在，求s的取值范围；若不存在，说明理由．

    查看答案和解析>>

    平面α，β，γ两两互相垂直，且交于点A，点B到α，β，γ的距离均为1，则A、B两点之间的距离|AB|=（　　）

    查看答案和解析>>

    平面内到定点（1，0）和到定点（4，0）的距离的比为
    1
    2
    的点的轨迹为曲线M，直线l与曲线M相交于A，B两点，若在曲线M上存在点C，使
    OC
    =
    OA
    +
    OB
    =λ
    a
    ，且
    a
    =(-1，2)    ，求直线l的斜率及对应的点C的坐标．

    查看答案和解析>>

    平面内动点P到点F（1，0）的距离等于它到直线x=-1的距离，记点P的轨迹为曲线Γ．
    （Ⅰ）求曲线Γ的方程；
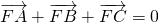    （Ⅱ）若点A，B，C是Γ上的不同三点，且满足数学公式．证明：△ABC不可能为直角三角形．

    查看答案和解析>>

    平面内到定点（1，0）和到定点（4，0）的距离的比为的点的轨迹为曲线M，直线l与曲线M相交于A，B两点，若在曲线M上存在点C，使，且=（-1，2），求直线l的斜率及对应的点C的坐标。

    查看答案和解析>>

    一、选择题（本大题共8小题,每小题5分,共40分）

    ACDDB CDC

     

    二、填空题（本大题共6小题，每小题5分.有两空的小题，第一空3分，第二空2分，共30分）

    （9）62        （10）2        （11）         （12）2，

    （13）    （14），③④

    三、解答题（本大题共6小题,共80分）

    (15)（本小题共13分）

    解：（Ⅰ）∵（），

    ∴（）.                ………………………………………1分

    ∵，，成等差数列，

    ∴.                                  ………………………………………3分

    ∴.                                     ………………………………………5分

    ∴.                                             ………………………………………6分

    （Ⅱ）由（Ⅰ）得

    （）.

    ∴数列为首项是，公差为1的等差数列.         ………………………………………8分

    ∴.

    ∴.                                         ………………………………………10分

    当时，.      ………………………………………12分

    当时，上式也成立.                             ………………………………………13分

    ∴（）.

     

    （16）（本小题共13分）

    解：（Ⅰ）该间教室两次检测中，空气质量均为A级的概率为.………………………………2分

    该间教室两次检测中，空气质量一次为A级，另一次为B级的概率为.

                                                              …………………………………4分

    设“该间教室的空气质量合格”为事件E.则                    …………………………………5分

    .                              …………………………………6分

    答：估计该间教室的空气质量合格的概率为.

    （Ⅱ）由题意可知，的取值为0，1，2，3，4.                …………………………………7分

    .

    随机变量的分布列为：

    0

    1

    2

    3

    4

                                                            …………………………………12分

    解法一：

    ∴.    …………………………………13分

    解法二：，

    ∴.                                       …………………………………13分

     

    （17）（本小题共14分）

    （Ⅰ）证明：设的中点为.

    在斜三棱柱中，点在底面上的射影恰好是的中点,

         平面ABC.         ……………………1分

    平面，

    .               ……………………2分

    ，

    ∴.

    ，

    ∴平面.       ……………………4分

    平面，

        平面平面.                          ………………………………………5分

    解法一：（Ⅱ）连接，平面，

    是直线在平面上的射影.          ………………………………………5分

    ，

    四边形是菱形.

    .                                   ………………………………………7分

    .                                   ………………………………………9分

    （Ⅲ）过点作交于点，连接.

    ，

    平面.

    .

    是二面角的平面角.               ………………………………………11分

    设，则，

    .

    .

    .

    .

    平面，平面，

    .

    .

    在中，可求.

    ∵，∴.

    ∴.

    .                   ………………………………………13分

    .

    ∴二面角的大小为.             ………………………………………14分

    解法二：（Ⅱ）因为点在底面上的射影是的中点，设的中点为，则平面ABC.以为原点，过平行于的直线为轴，所在直线为轴，所在直线为轴，建立如图所示的空间直角坐标系.

    设，由题意可知，.

    设，由，得

    ………………………………………7分

    .

      又.

    .

    .                                              ………………………………………9分

    （Ⅲ）设平面的法向量为.

    则

    ∴

    .

    设平面的法向量为.则

    ∴

    .                                   ………………………………………12分

    .                        ………………………………………13分

    二面角的大小为.           ………………………………………14分

    （18）（本小题共13分）

    解：（Ⅰ）函数的定义域为．                 ………………………………………1分

    .             ………………………………………3分

    由，解得.

    由，解得且．

    ∴的单调递增区间为，单调递减区间为，．

    ………………………………………6分

    （Ⅱ）由题意可知，，且在上的最小值小于等于时，存在实数，使得不等式成立．                             ………………………………………7分

    若即时，

    x

    a+1

    -

    0

    +

    ㄋ

    极小值

    ㄊ

    ∴在上的最小值为．

    则，得．                           ………………………………………10分

    若即时，在上单调递减，则在上的最小值为．

    由得（舍）．                            ………………………………………12分

    综上所述，．                               ………………………………………13分

    （19）（本小题共13分）

    解：（Ⅰ）由抛物线C:得抛物线的焦点坐标为，设直线的方程为：，.                                       ………………………………………1分

    由得.

    所以，.因为， …………………………………3分

    所以.

    所以.即.

    所以直线的方程为：或.           ………………………………………5分

    （Ⅱ）设，，则.

    由得.

    因为，所以，. ……………………………………7分

       （?）设，则.

      由题意知：∥，.

    即.

      显然      ………………………………………9分

    （?）由题意知：为等腰直角三角形，，即，即.

    . .

    .，.                      ………………………………………11分

      .

    即的取值范围是.                           ………………………………………13分

     

    （20）（本小题共14分）

    解：（Ⅰ）取，得，即.

    因为，所以.                         ………………………………………1分

    取，得.因为，所以.

    取，得

    同步练习册答案