
题目列表(包括答案和解析)
| OH |
| BG |
| EO |
| AE |
| OP |
| BG |
| 1 |
| 2 |
| 3 |

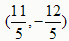 。
。 必过点C'。
必过点C'。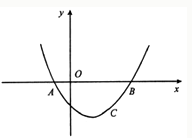
 过点(0,-2)且与x轴平行的直线,P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足.
过点(0,-2)且与x轴平行的直线,P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足.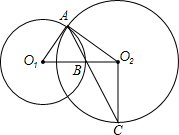 ⊙O2于点C,连接O2C.
⊙O2于点C,连接O2C. 如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.
如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com