
题目列表(包括答案和解析)
(本小题满分12分)
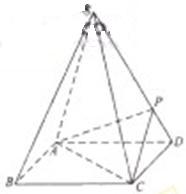
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的![]() 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
(本小题满分12分)如图,四棱锥![]() 中,侧面PDC是边长为2的正三角形,且与底面
中,侧面PDC是边长为2的正三角形,且与底面![]() 垂直,底面ABCD是面积为
垂直,底面ABCD是面积为![]() 的菱形,
的菱形,![]() 为锐角,M为PB的中点。
为锐角,M为PB的中点。
(1)求证![]()
(2)求二面角![]() 的大小
的大小
(3)求P到平面![]() 的距离
的距离
(本小题满分12分)
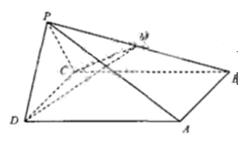
如图,四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB//CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() 。
。
(I)设M是PC上的一点,证明:平面MBD⊥平面PAD。
(II)求四棱锥P—ABCD的体积。
 (本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1) 求异面直线AF与BG所成的角的大小;
(2) 求平面APB与平面CPD所成的锐二面角的大小.
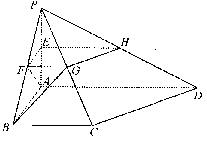 (本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1) 求异面直线AF与BG所成的角的大小;
(2) 求平面APB与平面CPD所成的锐二面角的大小.
2009年曲靖一中高考冲刺卷文科数学(一)
1.B 2.C 3.A 4.A 5.A 6.D 8.C 9.B 10.D 11.C 12.A
【解析】
1.依题意得 ,所以
,所以 故
故 且
且 ),因此选
),因此选

2.依题意得 又
又 在第二象限,所以
在第二象限,所以 ,
, ,故选C。
,故选C。
3. 且
且



4.过(-1,1)和(0,3)的直线方程为 ,令
,令 ,可得在
,可得在 轴的截距为
轴的截距为 ,故选A
,故选A
5.如图。





 故选A
故选A
6.设
则
 故选D
故选D
7.设等差数列 的首项为
的首项为 ,公差
,公差 ,因为
,因为 成等比数列,所以
成等比数列,所以 ,即
,即 ,解得
,解得 ,故选D
,故选D
8.由 ,所以
,所以 分
分 之比为2,设
之比为2,设 (
( ,
, 则
则 ,又点
,又点 在圆
在圆 上,所以
上,所以 ,即
,即 +
+ -4,化简得
-4,化简得 =16,故选C
=16,故选C
9.长方体的中心即为球心,设球半径为 ,则
,则


 于是
于是 两点的球面距离为
两点的球面距离为 故选B
故选B
10.画出 和
和
在 内的图象如图
内的图象如图

已知
 ,且两函数在
,且两函数在 上均为增函数,因此,两曲线在
上均为增函数,因此,两曲线在 内有一交点,故
内有一交点,故 与
与 的大小关系与
的大小关系与 的取值有关,故选D。
的取值有关,故选D。
11. 。而样本总容量为20。
。而样本总容量为20。
所以植物油类食品应抽取样本数为 ,果蔬类食品应抽取样本数为
,果蔬类食品应抽取样本数为 ,故,植物油类与果蔬类食品抽取的样本数之和为2+4=6,故应选C。
,故,植物油类与果蔬类食品抽取的样本数之和为2+4=6,故应选C。
12. 又因为对任意实数
又因为对任意实数 ,都有
,都有 即
即 ,
,
当且仅当 即
即 时,上述等号成立,即当
时,上述等号成立,即当 对,
对, 有最小值2,故选A。
有最小值2,故选A。
二、填空题
13.5.线性规划问题先作出可行域,注意本题已知最优的待定参数的特点,可考虑特殊的交点,再验证由题设可知
 ,应用运动变化的观点验证满足
,应用运动变化的观点验证满足 为所求。
为所求。
14.7.由题意得 又
又
因此A是钝角,
15.22,连接
 ,
,
 的周章为
的周章为
16.当 时,
时, ,取到最小值,因次,
,取到最小值,因次, 是对称轴:②当
是对称轴:②当 时,
时, 因此
因此 不是对称中心;③由
不是对称中心;③由 可得
可得 故
故 在
在 上不是增函数;④把函数
上不是增函数;④把函数 的图象向左平移
的图象向左平移 得到
得到
 的图象,得不到
的图象,得不到 的图象,故真命题序号是①。
的图象,故真命题序号是①。
三、解答题
17.(1) 在
在 上单调递增,
上单调递增, 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,
上恒成立, 即实数
即实数 的取值范围
的取值范围
(2)
 由题设条件知
由题设条件知 在
在 上单调递增。
上单调递增。
由 得
得 ,即
,即




即 的解集为
的解集为
又

 的解集为
的解集为
18.(1)过 作
作 子
子 连接
连接
 侧面
侧面
 。
。

 故
故 是边长为2的等边三角形。又
是边长为2的等边三角形。又 点,
点, 又
又 是
是 在底面
在底面 上的射影,
上的射影,
(法一)(2)
 就是二面角
就是二面角 的平面角,
的平面角, 和
和 都是边长为2的正三角形,
都是边长为2的正三角形, 又
又
 即二面角
即二面角 的大小为45°
的大小为45°
(3)取 的中点为
的中点为 连接
连接 又
又 为
为 的中点,
的中点, ,又
,又 ,且
,且 在平面
在平面 上,又
上,又 为
为 的中点,
的中点, 又
又

 线段
线段 的长就是
的长就是 到平面
到平面 的距离在等腰直角三角形
的距离在等腰直角三角形 中,
中, ,
, ,
, ,即
,即 到平面
到平面 的距离是
的距离是
(法二)(2) ,
, 以
以 为
为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,则点
轴建立空间直角坐标系,则点
 设平面
设平面 的法向量为
的法向量为 ,则
,则 ,解得
,解得 ,
, 取
取 则
则 ,平面
,平面 的法向量
的法向量

 向量
向量 所成角为45°故二面角
所成角为45°故二面角 的大小为45°,
的大小为45°,
(3)由 ,
, 的中点
的中点 设平面
设平面 的法向量为
的法向量为 ,则
,则 ,解得
,解得 则
则 故
故 到平面
到平面 的距离为
的距离为
19.(1)每天不超过20人排队结算的概率为:
(2)每天超过15分排队结算的概率为, 一周7天中,没有出现超过15分排队结算的概率为
一周7天中,没有出现超过15分排队结算的概率为
一周7天中,有一天出现超过15人排队结算的概率为
一周7天中,有两天出现超过15人排队结算的概率为
 一周7天中,有3天以上(含3天)出现超过15人跑队结算的概率为;
一周7天中,有3天以上(含3天)出现超过15人跑队结算的概率为;

所以,该商场需要增加结算窗口。
20.(1)由已知 得
得
又 因此
因此 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
(2)由(1)得


①式两边同乘以3,得 ②
②
①式-③式得,

21.(1)

即当 时
时 取得最小值
取得最小值 因斜率最小的切线与
因斜率最小的切线与 平行,即读切线的斜率为-12,所以
平行,即读切线的斜率为-12,所以 ,即
,即 ,由题设条件知
,由题设条件知
(2)由(1)知 ,因此
,因此

令 ,解得
,解得 当
当 时,
时, 故
故 在
在 上为增函数。当
上为增函数。当 时,
时, 故
故 在
在 上为减函数。
上为减函数。
当 时,
时, ,故
,故 在
在 上为增函数。
上为增函数。
由此可见,函数 的单调递增区间为(
的单调递增区间为( )和
)和 ,单调递减区间为
,单调递减区间为 。
。
22.(1)连接 ,由题意知:
,由题意知:




圆 为圆
为圆 的半径,
的半径,
又
 点
点 在
在 为焦点的椭圆上,即
为焦点的椭圆上,即
 点
点 的轨迹方程为
的轨迹方程为
(2)由 , 消去
, 消去 得1
得1
 由
由 得
得
设 则
则 ,有
,有


设点 到直线
到直线 的距离为
的距离为 ,则
,则


当 ,即
,即
 时,等号成立。
时,等号成立。

 面积的最大值为3
面积的最大值为3
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com