
题目列表(包括答案和解析)
 如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2.
如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2. |
| AN |
| 1 |
| 3 |
 |
| AB |
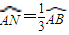 ,求面ANP与面POM所成角的正弦值.
,求面ANP与面POM所成角的正弦值.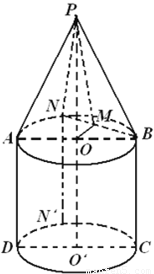
如图、椭圆![]() 的一个焦点是F(1,0),O为坐标原点.
的一个焦点是F(1,0),O为坐标原点.

(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F任意转动,值有|OA|2+|OB|2![]() |AB|2,求a的取值范围.
|AB|2,求a的取值范围.
(08年中卫一中三模理) (12分) 已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率等于
的焦点,离心率等于![]()
(I)求椭圆C的标准方程;
(II)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若
![]() 为定值.
为定值.
(本小题满分14分)椭圆![]() 的一个焦点是
的一个焦点是![]() ,
,![]() 为坐标原点(Ⅰ)已知椭圆短袖的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
为坐标原点(Ⅰ)已知椭圆短袖的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,若直线
两点,若直线![]() 绕点
绕点![]() 任意转动,恒有
任意转动,恒有![]() 求
求![]() 的取值范围.
的取值范围.
一、
1.D 2.C 3.B 4.D 5.C 6.A 7.D 8.B 9.C 10.C
11.D 12.A
【解析】
5.解: ,则
,则 .
.
6.解:线性规划问题可先作出可行域(略),设 ,则
,则 ,可知在点(1,1)处
,可知在点(1,1)处 取最小值,
取最小值, .
.
7.解: ,由条件知曲线在点(0,1)处的切线斜率为
,由条件知曲线在点(0,1)处的切线斜率为 ,则
,则 .
.
8.解:如图

正四棱锥 中,取
中,取 中点
中点 ,连接
,连接 、
、 ,易知
,易知 就是侧面与底面所成角,
就是侧面与底面所成角, 面
面 ,则
,则 .
.
9.解: ,展开式中含
,展开式中含 的项是
的项是 ,其系数是
,其系数是 .
.
10.解: ,其值域是
,其值域是 .
.
11.解: ,设离心率为
,设离心率为 ,则
,则 ,由
,由 知
知 .
.
12.解:如图

正四面体 中,
中, 是
是 中心,连
中心,连 ,此四面体内切球与外接球具有共同球心
,此四面体内切球与外接球具有共同球心 ,
, 必在
必在 上,并且
上,并且 等于内切球半径,
等于内切球半径, 等于外接球半径.记
等于外接球半径.记 面积为
面积为 ,则
,则
 ,从而
,从而

 .
.
二、填空题
13. .
.
解: ,
, 与
与 共线
共线 .
.
14.120种.
解:按要求分类相加,共有 种,或使用间接法:
种,或使用间接法: 种.
种.
15. .
.
解:曲线 ①,化作标准形式为
①,化作标准形式为 ,表示椭圆,由于对称性,取焦点
,表示椭圆,由于对称性,取焦点 ,过
,过 且倾角是135°的弦所在直线方程为:
且倾角是135°的弦所在直线方程为: ,即
,即 ②,联立式①与式②消去
②,联立式①与式②消去 得:
得:

 ,由弦长公式得:
,由弦长公式得: .
.
16.充要条件①:底面是正三角形,顶点在底面的射影恰是底面的中心.
充要条件②:底面是正三角形,且三条侧棱长相等,
再如:底面是正三角形,且三个侧面与底面所成角相等;底面是正三角形,且三条侧棱与底面所成角相等;三条侧棱长相等,且三个侧面与底面所成角相等;三个侧面与底面所成角相等,三个侧面两两所成二面角相等.
三、解答题
17.解:设等差数列 的公差为
的公差为 、
、 、
、 成等比数列,即
成等比数列,即 ,
,
 ,得
,得 或
或 .
.
 时
时 是常数列,
是常数列, ,前
,前 项和
项和
 时,
时, 的前
的前 项和
项和

 或
或 .
.
18.解: ,则
,则 ,
, ,
, .
.
由正弦定理得:
 ,
,
 ,则
,则

 .
.
19.解:已知甲击中9环、10环的概率分别是0.3、0.2,则甲击中8环及其以下环数的概率是0.5;乙击中9环、10环的概率分别为0.4、0.3,则乙击中8环及其以下环数的概率是0.3;丙击中9环、10环的概率是0.6、0.4,0.6+0.4=1,则丙击中8环及其以下环数是不可能事件.
(1)记在一轮比赛中“丙击中的环数不超过甲击中的环数”为事件 ,
, 包括“丙击中9环且甲击中9或10环”、“丙击中10环且甲击中10环”两个互斥事件,则
包括“丙击中9环且甲击中9或10环”、“丙击中10环且甲击中10环”两个互斥事件,则
 .
.
(2)记在一轮比赛中,“甲击中的环数超过丙击中的环数”为事件 ,“乙击中的环数超过丙击中的环数”为事件
,“乙击中的环数超过丙击中的环数”为事件 ,则
,则 与
与 相互独立,且
相互独立,且 ,
, .
.
所以在一轮比赛中,甲、乙击中的环数都没有超过丙击中的环数的概率为:

 .
.
20.(1)证:已知 是正三棱柱,取
是正三棱柱,取 中点
中点 ,
, 中点
中点 ,连
,连 ,
, ,则
,则 、
、 、
、 两两垂直,以
两两垂直,以 、
、 、
、 为
为 、
、 、
、 轴建立空间直角坐标系,又已知
轴建立空间直角坐标系,又已知 ,
,
则
 .
.

 ,
, ,则
,则 ,又因
,又因 与
与 相交,故
相交,故 面
面 .
.
(2)解:由(1)知, 是面
是面 的一个法向量.
的一个法向量.
 ,设
,设 是面
是面 的一个法向量,则
的一个法向量,则 ①,
①, ②,取
②,取 ,联立式①与式②解得
,联立式①与式②解得 ,则
,则 .
.
二面角 是锐二面角,记其大小为
是锐二面角,记其大小为 .则
.则
 ,
,
二面角 的大小
的大小 ,亦可用传统方法解决(略).
,亦可用传统方法解决(略).
21.解: .
.
(1) 在
在 处取得极值,则
处取得极值,则 .
.
(2) ,
,

恒成立, 必有解.
必有解.
易知函数 图象(抛物线)对称轴方程是
图象(抛物线)对称轴方程是 .
.
 在
在 上是增函数,则
上是增函数,则 时恒有
时恒有 ,进而必有(数形结合)
,进而必有(数形结合)
 或
或 或
或 ,
,
故 的取值范围是:
的取值范围是: .
.
22.解:(1)已知 ,求得线段
,求得线段 的两个三等分点
的两个三等分点 、
、 ,直线
,直线 过
过 时,
时, ,直线
,直线 过
过 时,
时, ,故
,故 或
或 .
.

(2)已知 是椭圆短轴端点和焦点,易求得椭圆方程是:
是椭圆短轴端点和焦点,易求得椭圆方程是: ,
, 所在直线的方程为
所在直线的方程为 .
.
直线与 椭圆相交于
椭圆相交于 、
、 ,设
,设 ,
, ,由直线
,由直线 与线段
与线段 相交(交点不与
相交(交点不与 、
、 重合)知
重合)知 .
.
点 在椭圆上,则
在椭圆上,则 ,解得
,解得 到直线
到直线 的距离
的距离
 ,
,
点 到直线
到直线 的距离;
的距离;

设 ,则
,则 ,由
,由 知
知 ,则:
,则:

 ,
,
当 即
即 时,
时, 取到最大值
取到最大值 .
.
www.ks5u.com ,0与
,0与 中,0距
中,0距 更远,当
更远,当 且
且 时,
时,
 ,
,
 .
.
∴四边形 的面积
的面积 ,当
,当 时,
时, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com