
题目列表(包括答案和解析)
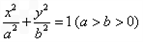 的左焦点为
的左焦点为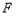
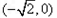 ,离心率e=
,离心率e=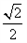 ,M、N是椭圆上的动点。
,M、N是椭圆上的动点。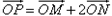 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为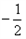 ,问:是否存在定点
,问:是否存在定点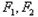 ,使得
,使得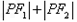 为定值?,若存在,求出
为定值?,若存在,求出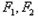 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。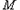 在第一象限,且点
在第一象限,且点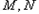 关于原点对称,点
关于原点对称,点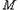 在
在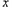 轴上的射影为
轴上的射影为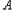 ,连接
,连接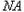 并延长交椭圆于点
并延长交椭圆于点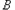 ,证明:
,证明: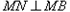 ;
; ,
,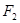 是椭圆
是椭圆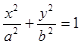
 左右焦点,它的离心率
左右焦点,它的离心率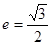 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为
 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求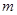 的取值范围。
的取值范围。已知 ,
, 是椭圆
是椭圆
 左右焦点,它的离心率
左右焦点,它的离心率 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为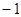
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求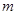 的取值范围。
的取值范围。
【解析】解:因为第一问中,利用椭圆的性质由 得
得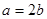 所以椭圆方程可设为:
所以椭圆方程可设为: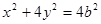 ,然后利用
,然后利用
得 得
得


 椭圆方程为
椭圆方程为
第二问中,当 为钝角时,
为钝角时, ,
得
,
得
所以 得
得
解:(Ⅰ)由 得
得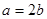 所以椭圆方程可设为:
所以椭圆方程可设为: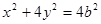
 3分
3分
得 得
得


 椭圆方程为
椭圆方程为 3分
3分
(Ⅱ)当 为钝角时,
为钝角时, ,
得
,
得 3分
3分
所以 得
得
已知 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P 在椭圆上,线段
在椭圆上,线段 与y轴的交点M满足
与y轴的交点M满足
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 圆O是以 为直径的圆,直线
为直径的圆,直线 :
: 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点 ,当
,当 ,且满足
,且满足 时,求直线
时,求直线 的方程。
的方程。
已知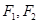 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P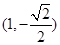 在椭圆上,线段
在椭圆上,线段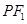 与y轴的交点M满足
与y轴的交点M满足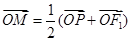
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 圆O是以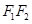 为直径的圆,直线
为直径的圆,直线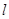 :
: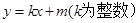 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点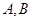 ,当
,当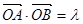 ,且满足
,且满足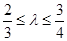 时,求直线
时,求直线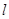 的方程。
的方程。
一、选择题(4′×10=40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空题(4′×4=16分)
11. 12.
12. 13.
13. 14.
14.
三、解答题(共44分)
15.①解:原不等式可化为: ………………………2′
………………………2′
 作根轴图:
作根轴图:
………………………4′
可得原不等式的解集为: ………………………6′
………………………6′
②解:直线 的斜率
的斜率 ………………………2′
………………………2′
∵直线 与该直线垂直
与该直线垂直
∴ ………………………4′
………………………4′
则 的方程为:
的方程为: ………………………5′
………………………5′
即 为所求………………………6′
为所求………………………6′
 16.解:∵
16.解:∵ ∴
∴ ,
, 且
且 ………………………1′
………………………1′
于是 ………………………3′
………………………3′
 ………………………4′
………………………4′
 ………………………5′
………………………5′

当且仅当: 即
即 ………………………6′
………………………6′
 时,
时, ………………………7′
………………………7′
17.解:将 代入
代入 中变形整理得:
中变形整理得:
 ………………………2′
………………………2′
首先
 且
且 ………………………3′
………………………3′
设

由题意得:
解得: 或
或 (舍去)………………………5′
(舍去)………………………5′
由弦长公式得: ………………………7′
………………………7′
18.解①设双曲线的实半轴,虚半轴分别为 ,
,

由题得: ∴
∴ ………………………1′
………………………1′
于是可设双曲线方程为: ………………………2′
………………………2′
将点 代入可得:
代入可得: ,
,
∴该双曲线的方程为: ………………………4′
………………………4′
②直线方程可化为: ,
,
则它所过定点 代入双曲线方程:
代入双曲线方程: 得:
得:

∴ ………………………6′
………………………6′
又由 得
得 ,
,
∴ ,
, 或
或 ,
, …………7′
…………7′
∴
∴ ……………………8′
……………………8′
19.解:①设中心 关于
关于 的对称点为
的对称点为 ,
,
则 解得:
解得:
∴ ,又点
,又点 在左准线
在左准线 上,
上, 轴
轴
∴ 的方程为:
的方程为: ……………………4′
……………………4′
②设 、
、 、
、 、
、
∵ 、
、 、
、 成等差数列,
成等差数列,
∴ ,
,
即:
亦:
∴ ……………………6′
……………………6′
 ∴
∴
由 得
得 ……………………8′
……………………8′
∴ , ∴
, ∴
又由 代入上式得:
代入上式得:
∴ ,
, ∴
∴ ……………………9′
……………………9′
∴ ,
, ,
,
∴椭圆的方程为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com