
题目列表(包括答案和解析)
若焦点在 轴上的椭圆
轴上的椭圆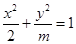 的离心率为
的离心率为 ,则
,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
若焦点在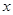 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
若焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 ( )
( )
A、 B、
B、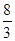 C、
C、 D、
D、
若焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( )
A. B.
B.
 C.
C.
 D.
D.

若焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
一、选择题(本大题共8小题,每小题5分,共40分)
1.D 2.C 3.B 4.B 5.D 6.D 7.A 8.C
二、填空题(本大题共6小题,每小题5分,共30分)
9.72 10..files/image148.gif) 11.1 ,
11.1 ,.files/image150.gif) 12.f(x)=
12.f(x)=.files/image152.gif) ,3
,3
13..files/image154.gif) ,
,.files/image156.gif) 14.①②
14.①②.files/image158.gif) ③④ , ①③
③④ , ①③.files/image158.gif) ②④
②④
注:两个空的填空题第一个空填对得2分,第二个空填对得3分.
三、解答题(本大题共6小题,共80分)
15.(本小题满分13分)
解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是
(7-2 x)人.
(I)∵.files/image160.gif) ,
,
∴.files/image162.gif) .……………………………………3分
.……………………………………3分
即.files/image164.gif) .
.
∴.files/image166.gif) .
.
∴x=2. ……………………………………5分
故文娱队共有5人.……………………………………7分
(II) .files/image093.gif) 的概率分布列为
的概率分布列为
.files/image093.gif)
0
1
2
P
.files/image168.gif)
.files/image170.gif)
.files/image172.gif)
.files/image174.gif) ,……………………………………9分
,……………………………………9分
.files/image176.gif) ,……………………………………11分
,……………………………………11分
∴.files/image178.gif) =1. …………………………13分
=1. …………………………13分
16.(本小题满分13分)
解:(I)由.files/image100.gif) ,得
,得
.files/image180.gif) .……………………………………2分
.……………………………………2分
当x=1时,切线l的斜率为3,可得
当.files/image106.gif) 时,
时,.files/image108.gif) 有极值,则
有极值,则.files/image182.gif) ,可得
,可得
由①、②解得 a=2,b=-4.……………………………………5分
设切线l的方程为 .files/image184.gif) .
.
由原点到切线l的距离为.files/image104.gif) ,
,
则.files/image186.gif) .解得m=±1.
.解得m=±1.
∵切线l不过第四象限,
∴m=1.……………………………………6分
由于l切点的横坐标为x=1,∴.files/image188.gif) .
.
∴1+a+b+c=4.
∴c=5.…………………………………………………………………7分
(II)由(I)可得.files/image190.gif) ,
,
∴.files/image192.gif) .……………………………………8分
.……………………………………8分
令.files/image194.gif) ,得x=-2,
,得x=-2, .files/image106.gif) .
.
x
[-3,-2)
-2
(-2, .files/image196.gif) )
)
.files/image196.gif)
(.files/image196.gif) ,1]
,1]
.files/image199.gif)
+
0
-
0
+
f(x)
.files/image200.gif)
.files/image201.gif)
极大值
.files/image202.gif)
.files/image203.gif)
极小值
.files/image204.gif)
.files/image201.gif)
……………………………………11分
∴f(x)在x=-2处取得极大值f(-2)=13.
在.files/image106.gif) 处取得极小值
处取得极小值.files/image206.gif) =
=.files/image208.gif) .
.
又f(-3)=8,f(1)=4.
∴f(x)在[-3,1]上的最大值为13,最小值为.files/image208.gif) .……………………………………13分
.……………………………………13分
17.(本小题满分14分)
解法一:(I) ∵PC.files/image110.gif) 平面ABC,
平面ABC,.files/image210.gif) 平面ABC,
平面ABC,
∴PC.files/image110.gif) AB.…………………………2分
AB.…………………………2分
.files/image212.gif) ∵CD
∵CD.files/image110.gif) 平面PAB,
平面PAB,.files/image210.gif) 平面PAB,
平面PAB,
∴CD.files/image110.gif) AB.…………………………4分
AB.…………………………4分
又.files/image215.gif) ,
,
∴AB.files/image110.gif) 平面PCB. …………………………5分
平面PCB. …………………………5分
(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则.files/image217.gif) 为异面直线PA与BC所成的角.………6分
为异面直线PA与BC所成的角.………6分
由(Ⅰ)可得AB⊥BC,
∴CF.files/image110.gif) AF.
AF.
由三垂线定理,得PF.files/image110.gif) AF.
AF.
则AF=CF=.files/image219.gif) ,PF=
,PF=.files/image221.gif) ,
,
在.files/image223.gif) 中, tan∠PAF=
中, tan∠PAF=.files/image225.gif) =
=.files/image227.gif) ,
,
∴异面直线PA与BC所成的角为.files/image229.gif) .…………………………………9分
.…………………………………9分
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE .files/image110.gif) PA,CE=
PA,CE=.files/image219.gif) .
.
∵CD.files/image110.gif) 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE .files/image110.gif) PA.
PA.
∴.files/image231.gif) 为二面角C-PA-B的平面角.…………………………………11分
为二面角C-PA-B的平面角.…………………………………11分
由(I) AB.files/image110.gif) 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=.files/image219.gif) .
.
在.files/image233.gif) 中,PB=
中,PB=.files/image235.gif) ,
,
.files/image237.gif) .
.
.files/image239.gif) 在
在.files/image241.gif) 中, sin∠CED=
中, sin∠CED=.files/image243.gif) .
.
∴二面角C-PA-B的大小为arcsin.files/image245.gif) .……14分
.……14分
解法二:(I)同解法一.
(II) 由(I) AB.files/image110.gif) 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=.files/image219.gif) .
.
以B为原点,如图建立坐标系.
则A(0,.files/image219.gif) ,0),B(0,0,0),
,0),B(0,0,0),
C(.files/image219.gif) ,0,0),P(
,0,0),P(.files/image219.gif) ,0,2).
,0,2).
.files/image248.gif) ,
,.files/image250.gif) .
.
…………………7分
则.files/image252.gif) +0+0=2.
+0+0=2.
.files/image254.gif) =
=.files/image256.gif) =
= .files/image073.gif) .
.
∴异面直线AP与BC所成的角为.files/image229.gif) .………………………10分
.………………………10分
(III)设平面PAB的法向量为m= (x,y,z).
.files/image260.gif) ,
,.files/image248.gif) ,
,
则.files/image262.gif) 即
即.files/image264.gif)
.files/image266.gif)
解得.files/image268.gif) 令
令.files/image270.gif) = -1, 得 m= (
= -1, 得 m= (.files/image219.gif) ,0,-1).
,0,-1).
设平面PAC的法向量为n=(.files/image272.gif) ).
).
.files/image274.gif) ,
,.files/image276.gif) ,
,
则.files/image278.gif) 即
即.files/image280.gif)
解得.files/image282.gif) 令
令.files/image284.gif) =1, 得 n= (1,1,0).……………………………12分
=1, 得 n= (1,1,0).……………………………12分
.files/image286.gif) =
=.files/image288.gif) .
.
∴二面角C-PA-B的大小为arccos.files/image290.gif) .………………………………14分
.………………………………14分
18.(本小题满分13分)
解:(I)设P(x,y),因为A、B分别为直线.files/image114.gif) 和
和.files/image116.gif) 上的点,故可设
上的点,故可设
.files/image292.gif) ,
,.files/image294.gif) .
.
∵.files/image120.gif) ,
,
∴.files/image296.gif) ∴
∴.files/image298.gif) ………………………4分
………………………4分
又.files/image300.gif) ,
,
∴.files/image302.gif) .……………………………………5分
.……………………………………5分
∴.files/image304.gif) .
.
即曲线C的方程为.files/image306.gif) .………………………………………6分
.………………………………………6分
(II) 设N(s,t),M(x,y),则由.files/image122.gif) ,可得(x,y-16)=
,可得(x,y-16)=.files/image124.gif) (s,t-16).
(s,t-16).
故.files/image308.gif) ,
,.files/image310.gif) .……………………………………8分
.……………………………………8分
∵M、N在曲线C上,
∴.files/image312.gif) ……………………………………9分
……………………………………9分
消去s得 .files/image314.gif) .
.
由题意知.files/image316.gif) ,且
,且.files/image318.gif) ,
,
解得 .files/image320.gif) .………………………………………………………11分
.………………………………………………………11分
又 .files/image322.gif) , ∴
, ∴.files/image324.gif) .
.
解得
.files/image326.gif) (
(.files/image318.gif) ).
).
故实数.files/image124.gif) 的取值范围是
的取值范围是.files/image326.gif) (
(.files/image318.gif) ).………………………………13分
).………………………………13分
19.(本小题满分13分)
解:(I)∵.files/image134.gif) ,
,.files/image330.gif) ,
,.files/image332.gif) ,
,
∴.files/image334.gif) .
.
即.files/image336.gif) .
.
又.files/image132.gif) ,可知对任何
,可知对任何.files/image338.gif) ,
,.files/image340.gif) ,
,
所以.files/image342.gif) .……………………………2分
.……………………………2分
∵.files/image344.gif) ,
,
∴.files/image138.gif) 是以
是以.files/image346.gif) 为首项,公比为
为首项,公比为.files/image348.gif) 的等比数列.………4分
的等比数列.………4分
(II)由(I)可知.files/image350.gif) =
=.files/image352.gif) (
(.files/image354.gif) ).
).
∴.files/image356.gif) .
.
.files/image358.gif) .……………………………5分
.……………………………5分
当n=7时,.files/image360.gif) ,
,.files/image362.gif) ;
;
当n<7时,.files/image364.gif) ,
,.files/image366.gif) ;
;
当n>7时,.files/image368.gif) ,
,.files/image370.gif) .
.
∴当n=7或n=8时,.files/image140.gif) 取最大值,最大值为
取最大值,最大值为.files/image373.gif) .……8分
.……8分
(III)由.files/image142.gif) ,得
,得.files/image376.gif) (*)
(*)
依题意(*)式对任意.files/image144.gif) 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.…………9分
②当t<0时,由.files/image378.gif) ,可知
,可知.files/image380.gif) (
(.files/image144.gif) ).
).
而当m是偶数时.files/image382.gif) ,因此t<0不合题意.…………10分
,因此t<0不合题意.…………10分
③当t>0时,由.files/image382.gif) (
(.files/image144.gif) ),
),
∴.files/image385.gif) ∴
∴.files/image387.gif) . (
. (.files/image144.gif) )……11分
)……11分
设.files/image389.gif) (
(.files/image144.gif) )
)
∵.files/image391.gif) =
=.files/image393.gif) ,
,
∴.files/image395.gif) .
.
∴.files/image397.gif) 的最大值为
的最大值为.files/image399.gif) .
.
所以实数.files/image401.gif) 的取值范围是
的取值范围是.files/image403.gif) .…………………………………13分
.…………………………………13分
20.(本小题满分14分)
解:(I) ∵x>0,∴.files/image405.gif)
∴f(x)在(0,1)上为减函数,在.files/image407.gif) 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),
可得 0<a.files/image409.gif) 1<b和
1<b和.files/image411.gif) .
.
即.files/image413.gif) .
.
∴2ab=a+b>.files/image415.gif) .……………………………………3分
.……………………………………3分
故.files/image417.gif) ,即ab>1.……………………………………4分
,即ab>1.……………………………………4分
(II)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=.files/image146.gif) 的定义域、值域都是
的定义域、值域都是
[a,b],则a>0.
.files/image405.gif)
① 当.files/image419.gif) 时,
时,.files/image421.gif) 在(0,1)上为减函数.
在(0,1)上为减函数.
故.files/image423.gif) 即
即 .files/image425.gif)
解得 a=b.
故此时不存在适合条件的实数a,b.………………………………6分
② 当.files/image427.gif) 时,
时,.files/image429.gif) 在
在.files/image407.gif) 上是增函数.
上是增函数.
故.files/image432.gif) 即
即 .files/image434.gif)
此时a,b是方程.files/image436.gif) 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数a,b.………………………………8分
③ 当.files/image438.gif) ,
,.files/image440.gif) 时,
时,
由于.files/image442.gif) ,而
,而.files/image444.gif) ,
,
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.………………………………10分
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
① 当.files/image419.gif) 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故.files/image446.gif) .此时刻得a,b异号,不符合题意,所以a,b不存在.
.此时刻得a,b异号,不符合题意,所以a,b不存在.
② 当.files/image438.gif) 或
或.files/image440.gif) 时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有.files/image427.gif) .
.
∵.files/image146.gif) 在
在.files/image448.gif) 上是增函数,
上是增函数,
∴.files/image450.gif) 即
即 .files/image452.gif)
a, b是方程.files/image454.gif) 的两个根.
的两个根.
即关于x的方程.files/image454.gif) 有两个大于1的实根.……………………12分
有两个大于1的实根.……………………12分
设这两个根为.files/image457.gif) ,
,.files/image459.gif) .
.
则.files/image457.gif) +
+.files/image459.gif) =
=.files/image463.gif) ,
,.files/image457.gif) ?
?.files/image459.gif) =
=.files/image463.gif) .
.
∴.files/image465.gif) 即
即 .files/image467.gif)
解得 .files/image469.gif) .
.
故m的取值范围是.files/image469.gif) .…………………………………………14分
.…………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com