题目列表(包括答案和解析)
已知
（I）求数列{
}的通项公式；
（II）数列{
}的首项b1=1，前n项和为Tn，且
，求数列{}的通项公式bn.
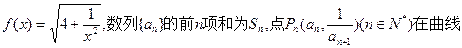
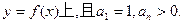
}的通项公式；
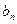}的首项b1=1，前n项和为Tn，且
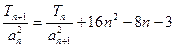，求数列{}的通项公式bn.已知
，
（I）求数列
的通项公式；
（II）设各项均为正数的等比数列
成等差数列，求Tn.
已知
，
（I）求数列
的通项公式；
（II）设各项均为正数的等比数列
成等差数列，求Tn.
在数列
（I）求数列
的通项公式；
（II）设
；
（III）设
，是否存在整数m，使得对任意
成立？若存在，求出m的最大值；若不存在，请说明理由.
一、选择题
1―10 ACBCB DBCDD
二、填空题
11．
12．
13．―3 14．
15．2 16．
17．<
三、解答题：
18．解：（I）
（II）由于区间
的长度是为
，为半个周期。
又
分别取到函数的最小值
所以函数
上的值域为
。……14分
19．解：（Ⅰ）证明：连接BD，设AC与BD相交于点F．
因为四边形ABCD是菱形，所以AC⊥BD．……………………2分
又因为PD⊥平面ABCD，AC
平面ABCD，所以PD⊥AC．………………4分
而AC∩BD＝F，所以AC⊥平面PDB．
E为PB上任意一点，DE平面PBD，所以AC⊥DE．……………………6分
（Ⅱ）连EF．由（Ⅰ），知AC⊥平面PDB，EF平面PBD，所以AC⊥EF．
S△ACE =
AC?EF，在△ACE面积最小时，EF最小，则EF⊥PB．
S△ACE=9，×6×EF＝9，解得EF＝3． …………………8分
由PB⊥EF且PB⊥AC得PB⊥平面AEC，则PB⊥EC，
又由EF=AF=FC=3，得EC⊥AE，而PB∩AE=E，故EC⊥平面PAB。………10分
作GH//CE交PB于点G，则GH⊥平面PAB，
所以∠GEH就是EG与平面PAB所成角。 ………………12分
在直角三角形CEB中，BC=6，
|
………………5分
………………6分
………………6分
要使对任意
………………14分
到焦点F的距离是
…………4分
轴不平行，
时，不存在这样的直线l；
………………16分