
题目列表(包括答案和解析)
 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图:则四棱锥P-ABCD的表面积为
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图:则四棱锥P-ABCD的表面积为 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )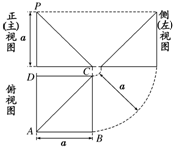 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图,则四棱锥P-ABCD的表面积为.( )
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图,则四棱锥P-ABCD的表面积为.( )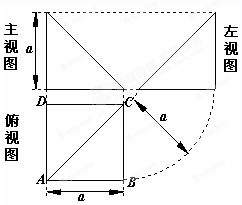 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图
 )a2
)a2 )a2
)a2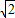 )
) )π
)π一、选择题:
1―5 ACBBD 6―10 BCDAC
二、填空题:
11.60 12. 13.―
13.― 14.
14.
15.2 16. 17.
17.
三、解答题:
18.解:(I)
|