(本小题满分12分) 设{a_n}是等差数列，{b_n}是各项都为正数的等比数列，且a₁=b₁=1，a₃+b₅=21，a₅+b₃=13.

(1)求{a_n}，{b_n}的通项公式；         

(2)求数列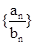的前n项和S_n.

(本小题满分12分)

某班甲、乙两名同学参加l00米达标训练，在相同条件下两人l0次训练的成绩(单位：秒)如下：

(I)请作出样本数据的茎叶图；如果从甲、乙两名同学中选一名参加学校的100米比赛，从成绩的稳定性方面考虑，选派谁参加比赛更好，并说明理由(不用计算，可通过统计图直接回答结论)．

(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次，求抽取的成绩中至少有一个比12．8秒差的概率．

(Ⅲ)经过对甲、乙两位同学的多次成绩的统计，甲、乙的成绩都均匀分布在[11．5，14．5]

之间，现甲、乙比赛一次，求甲、乙成绩之差的绝对值小于0．8秒的概率．

（本小题满分12分）已知数列为等差数列，且为等比数列，数列的前三项依次为3，7，13。求
（Ⅰ）数列的通项公式；
（Ⅱ）数列的前项和

（本小题满分12分）设递增等比数列{}的前n项和为，且＝3，＝13，数列{}满足＝，点P（，）在直线x－y＋2＝0上，n∈N﹡
（Ⅰ）求数列{}，{}的通项公式
（Ⅱ）设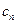＝，数列{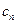}的前n项和，若>2a－1恒成立（n∈N﹡），求实数a的取值范围．

（本小题满分12分）
设{a_n}是等差数列，{b_n}是各项为正项的等比数列，且a₁=b₁="1," a₃+b₅="21," a₅+b₃=13.
(1)求{a_n},  {b_n}的通项公式；
（2）求数列{}的前n项和S_n;