
题目列表(包括答案和解析)
(本题16分)
如图所示,某人在斜坡P处仰视正对面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
轴正向,建立直角坐标系,求出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).

(本题满分16分)如图所示,在一张边长为20cm的正方形铁皮的4个角上,各剪去一个边长是 cm的小正方形,折成一个容积是
cm的小正方形,折成一个容积是 的无盖长方体铁盒,试写出用
的无盖长方体铁盒,试写出用 表示
表示 的函数关系式,并指出它的定义域。
的函数关系式,并指出它的定义域。

(本题16分)
如图所示,某人在斜坡P处仰视正对![]() 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为![]() ,
,![]()
(1)以射线OC为![]() 轴的正向,OB为
轴的正向,OB为![]() 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求![]() 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).

(本小题16分)如图所示,数列 的前
的前 项的和
项的和 ,
, 为数列
为数列 的前
的前 项的和,且
项的和,且 .
.

(1)求数列 、
、 的通项公式;
的通项公式;
(2)找出所有满足: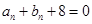 的自然数
的自然数 的值(不必证明);
的值(不必证明);
(3)若不等式 对于任意的
对于任意的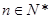 ,
, 恒成立,求实数
恒成立,求实数 的最小值,并求出此时相应的
的最小值,并求出此时相应的 的值.
的值.
(本题16分)
如图所示,某人在斜坡P处仰视正对 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com