
题目列表(包括答案和解析)
| 病症及代号 | 普通病症A1 | 复诊病症A2 | 常见病症A3 | 疑难病症A4 | 特殊病症A5 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间 (单位:分钟) |
3 | 4 | 5 | 6 | 7 |
解析:本例主要是培养学生理解概念的程度,了解解决数学问题都需要算法
算法一:按照逐一相加的程序进行.
第一步 计算1+2,得到3;
第二步 将第一步中的运算结果3与3相加,得到6;
第三步 将第二步中的运算结果6与4相加,得到10;
第四步 将第三步中的运算结果10与5相加,得到15;
第五步 将第四步中的运算结果15与6相加,得到21;
第六步 将第五步中的运算结果21与7相加,得到28.
算法二:可以运用公式1+2+3+…+n=![]() 直接计算.
直接计算.
第一步 取n=7;
第二步 计算![]() ;
;
第三步 输出运算结果.
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
|
病症及代号 |
普通病症 |
复诊病症 |
常见病症 |
疑难病症 |
特殊病症 |
|
人数 |
100 |
300 |
200 |
300 |
100 |
|
每人就诊时间(单位:分钟) |
3 |
4 |
5 |
6 |
7 |
用 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求 的数学期望.
的数学期望.
并以此估计专家一上午(按3小时计算)可诊断多少病人;
某病人按序号排在第三号就诊,设他等待的时间为 ,求
,求 ;
;
求专家诊断完三个病人恰好用了一刻钟的概率.
(由理科第三册§4.2例3改编)计算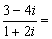 ( )
( )
A.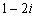 B.
B.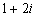 C.
C.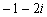 D.
D.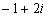
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 | 普通病症 | 复诊病症 | 常见病症 | 疑难病症 | 特殊病症 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间(单位:分钟) | 3 | 4 | 5 | 6 | 7 |
(1) 用![]() 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求![]() 的数学期望.
的数学期望.
并以此估计专家一上午(按3小时计算)可诊断多少病人;
(2) 某病人按序号排在第三号就诊,设他等待的时间为![]() ,求
,求![]() ;
;
(3) 求专家诊断完三个病人恰好用了一刻钟的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com