
题目列表(包括答案和解析)
在△ABC中,已知b,a,c成等差数列,b,a,c成等比数列.
(1)求证:△ABC是正三角形;
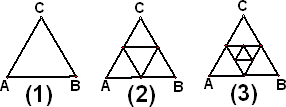
(2)如图(1),若△ABC为第一个三角形,分别连结△ABC三边的中点,将△ABC剖分成4个三角形(如图(2)),再分别连结图(2)中间的一个小三角形三边的中点,又可将△ABC剖分成7个三角形(如图(3)).依此类推,第n个图中△ABC被剖分为an个三角形,求an.
解:
 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (θ为参数),则圆C的普通方程为________.
(θ为参数),则圆C的普通方程为________.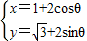 (θ为参数),则圆C的普通方程为 .
(θ为参数),则圆C的普通方程为 .
 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
|
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
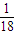 x2-
x2- x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC、现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC、现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒) )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;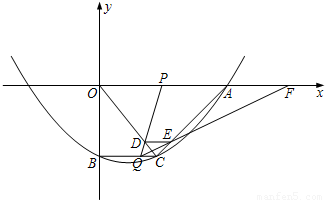
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com