练习册

  • 练习册
  • 试题
    19．(1)方法一:如图.以线段的中点为原点. 以线段所在的直线为轴建立直角坐标系． 则.． -----------2分 设动点的坐标为.则动点的坐标为 .. ----2分 由.得.-2分 方法二:由得.．----------2分 所以.动点的轨迹是抛物线.以线段的中点 为原点.以线段所在的直线为轴建立直角坐标系.可得轨迹的方程为:．----------------------4分 (2)方法一:如图.设直线的方程为...--1分 则. -----------------------------1分 联立方程组消去得. ..故 ----------------1分 -----------------------------1分 由.得. ..--------------------2分 整理得... .-------4分 方法二:由已知..得. -------2分 于是.. ① -------------------3分 如图.过.两点分别作准线的垂线.垂足分别为.. 则有 ② -------------------3分 由①.②得.-------------------------2分 【查看更多】

     

    题目列表(包括答案和解析)

    41、如图，在1×6的矩形长条格中，两格涂红色，两格涂黄色，两格涂蓝色，但要求至少有一种颜色涂在了相邻的两格，则不同的涂色方法共有
    60
    种

    查看答案和解析>>

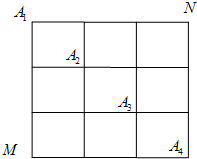    精英家教网如图，在某城市中，M，N两地之间有整齐的方格形道路网，其中A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处．今在道路网M，N处的甲、乙两人分别要到N，M处，他们分别随机地选择一条沿街的最短路径，以相同的速度同时出发，直到到达N，M为止．
    （1）求甲经过A2到达N的方法有多少种；
    （2）求甲、乙两人在A2处相遇的概率；
    （3）求甲、乙两人相遇的概率．

    查看答案和解析>>

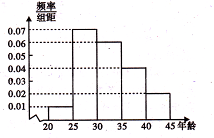    （2013•内江一模）某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．把符合条件的1000名志愿者按年龄分组：第1组[20，25）、第2组[25，30）、第3组[30，35）、第4组[35，40）、第5组[40，45），得到的频率分布直方图如图所示：
    （1）若从第3、4、5组中用分层抽样的方法抽取12名志愿者参加广场的宣传活动，应从第3、4、5组各抽取多少名志愿者？
    （2）在（1）的条件下，该市决定在这12名志愿者中随机抽取3名志愿者介绍宣传经验求第4组至少有一名志愿者被抽中的概率；
    （3）在（2）的条件下，若ξ表示抽出的3名志愿者中第3组的人数，求ξ的分布列和数学期望．

    查看答案和解析>>

    （2013•大连一模）如图是用模拟方法估计椭圆
    x2
    4
    +y2=1    面积的程序框图，S表示估计的结果，则图中空白处应该填入（　　）

    查看答案和解析>>

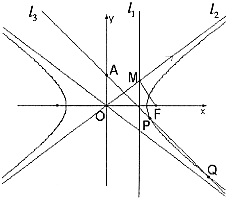    如图，已知双曲线C：
    x2
    a2
    -
    y2
    b2
    =1(a＞0，b＞0)    的右准线l1与一条渐近线l2交于点M，F是双曲线C的右焦点，O为坐标原点．
    （I）求证：
    OM
    ⊥
    MF
    ；
    （II）若|
    MF
    |=1且双曲线C的离心率e=
    		6
    2
    ，求双曲线C的方程；
    （III）在（II）的条件下，直线l3过点A（0，1）与双曲线C右支交于不同的两点P、Q且P在A、Q之间，满足
    AP
    =λ
    AQ
    ，试判断λ的范围，并用代数方法给出证明．

    查看答案和解析>>


    同步练习册答案