练习册

  • 练习册
  • 试题
    于是时.成立 【查看更多】

     

    题目列表(包括答案和解析)

    当时，关于x的不等式恒成立，则实数的取值范围是      ．

    查看答案和解析>>

    完成下列问题：

    (1)甲、乙两射手同时射击一目标，甲的命中率为0.65，乙的命中率为0.60，那么能否得出结论：目标被命中的概率等于0.65＋0.60＝1.25？

    (2)一射手命中靶的内圈的概率是0.25，命中靶的其余部分的概率是0.50．那么能否得出结论：目标被命中的概率等于0.25＋0.50＝0.75？

    (3)两人各掷一枚硬币，“同时出现正面”的概率可以算得为．由于“不出现正面”是上述事件的对立事件，所以它的概率等于1－＝．这样说对吗？

    查看答案和解析>>

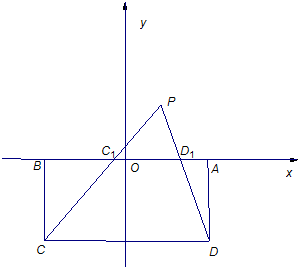    如图，矩形ABCD中，|AB|=10，|BC|=6，现以矩形ABCD的AB边为x轴，AB的中点为原点建立直角坐标系，P是x轴上方一点，使得PC、PD与线段AB分别交于点C1、D1，且|AD1|，|D1C1|，|C1B|成等比数列．
    （1）求动点P的轨迹方程；
    （2）求动点P到直线l：x+y+6=0距离的最大值及取得最大值时点P的坐标．

    查看答案和解析>>

    如图，弯曲的河流是近似的抛物线C，公路l恰好是C的准线，C上的点O到l的距离最近，且为0.4千米，城镇P位于点O的北偏东30°处，|OP|=10千米，现要在河岸边的某处修建一座码头，并修建两条公路，一条连接城镇，一条垂直连接公路l，以便建立水陆交通网．
    （1）建立适当的坐标系，求抛物线C的方程；
    （2）为了降低修路成本，必须使修建的两条公路总长最小，请给出修建方案（作出图形，在图中标出此时码头Q的位置），并求公路总长的最小值（精确到0.001千米）

    查看答案和解析>>

    对于函数，若存在实数，使成立，则称为的不动点.

     （1）当时，求的不动点；

     （2）若对于任何实数，函数恒有两相异的不动点，求实数的取值范围；

     （3）在（2）的条件下，若的图象上、两点的横坐标是函数的不动点，且直线是线段的垂直平分线，求实数的最小值.

    查看答案和解析>>


    同步练习册答案