练习册

  • 练习册
  • 试题
    20．观察下表:1.2.3.4.5.6.7.8.9.10.11.1213.14.15.16.17.18.19.20.21.22--解答下列问题: (1)此表中第10行的第10个数是几? (2)2008是此表中第几行的第几个数? 是否存在n∈N+.使得从第n行起的连续3行的所有数之和为626?若存在.求出n的值,若不存在.请说明理由. 100080已知点F(1.0).点P在y轴上运动.点M在x轴上运动. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）
    雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本，其选报文科理科的情况如下表所示。

     
    男
    女
    文科
    2
    5
    理科
    10
    3
    （Ⅰ）若在该样本中从报考文科的学生中随机地选出3人召开座谈会，试求3人中既有男生也有女生的概率；
    （Ⅱ）用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关？
    参考公式和数据：

    		0.15
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

    		2.07
    		2.71
    		3.84
    		5.02
    		6.64
    		7.88
    		10.83

    查看答案和解析>>

    (本小题满分12分）（文科做前两问；理科全做．）

    某会议室用3盏灯照明，每盏灯各使用节能灯棍一只，且型号相同．假定每盏灯能否正常照明只与灯棍的寿命有关，该型号的灯棍寿命为1年以上的概率为0.8，寿命为2年以上的概率为0.3，从使用之日起每满1年进行一次灯棍更换工作，只更换已坏的灯棍，平时不换．

    （I）在第一次灯棍更换工作中，求不需要更换灯棍的概率；

    （II）在第二次灯棍更换工作中，对其中的某一盏灯来说，求该灯需要更换灯棍的概率；

    （III）设在第二次灯棍更换工作中，需要更换的灯棍数为ξ，求ξ的分布列和期望．

     

     

    查看答案和解析>>

    (本小题满分12分）（文科做前两问；理科全做．）
    某会议室用3盏灯照明，每盏灯各使用节能灯棍一只，且型号相同．假定每盏灯能否正常照明只与灯棍的寿命有关，该型号的灯棍寿命为1年以上的概率为0.8，寿命为2年以上的概率为0.3，从使用之日起每满1年进行一次灯棍更换工作，只更换已坏的灯棍，平时不换．
    （I）在第一次灯棍更换工作中，求不需要更换灯棍的概率；
    （II）在第二次灯棍更换工作中，对其中的某一盏灯来说，求该灯需要更换灯棍的概率；
    （III）设在第二次灯棍更换工作中，需要更换的灯棍数为ξ，求ξ的分布列和期望．

    查看答案和解析>>

    (本题满分12分）已知椭圆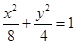，过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求：

    （1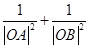）的值

    （2）判定直线AB与圆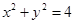的位置关系

    （文科）（3）求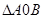面积的最小值

    （理科）（3）求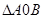面积的最大值

     

    查看答案和解析>>

    (本小题满分12分)

        某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生，

    其中8名女生中有3名报考理科，男生中有2名报考文科

       （1）是根据以上信息，写出列联表

       （2）用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关？参考公式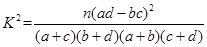

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

     

    2.07

    2.71

    3.84

    5.02

    6.64

    7.88

    10.83

     

     

    查看答案和解析>>

    一、选择题（本大题共12小题，每题5分，共60分，在每小题的选项中，只有一项符合）

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    C

    A

    C

    B

    B

    A

    D

    B

    D

    A

    C

    理D

    文C

    二、填空题：本大题共4小题，每小题4分，共16分

    13．（?∞，?2）    14．（理）：15    文：（－1，0）∪（0，1）

    15．2               16．①②③④

    三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。

    17．（12分）

       （1）

                 =……………………………………2分

                 =………………………………………………4分

    令………………………………6分

    得f（x）的减区间：………………8分

       （2）f（x）按平移后：

            …………………………………………10分

    要使g（x）为偶函数，则

    100080

    18．（12分）

       （1）马琳胜出有两种情况，3：1或3：2

            ………………………… 6分

       （2）

           

    分布列：    3      4     5

          P              ……………………10分

    E= ………………………………………………12分

    文科：前3次中奖的概率

    ……………………6分

    （2）在本次活动中未中奖的概率为

      （1－p）10…………………………………………………………8分

    恰在第10次中奖的概率为

    （1－p）9p………………………………………………………………10分

    ………………………………12分

    19．（12分）

    EM是平行四边形 …… 3分

    平面PAB ……5分

    （2）过Q做QF//PA  交AD于F

     QF⊥平面ABCD

    作FH⊥AC  H为垂足

    ∠QHF是Q―AC―D的平面角……8分

    设AF=x  则

    FD=2－x

    由

    在Rt△QFH中，

    ……10分

    ∴Q为PD中点……12分

    解法2

    （1）如图所示A（0，0，0）  B（1，0，0）C（1，1，0）D（0，2，0） p（0，0，1）

     M（0，1，……………………………………3分

    是平面PAB的法向量  

        故MC//平面PAB…………5分

    （2）设

    设是平面QAC的法向量

    由………………………………9分

    又为平面ACD的法向量，于是

    ∴Q为PD的中点…………………………………………12分

    20．经分析可知第n行有3n－2个数，                  理科        文科

    前n－１行有                    

    第n行的第1个数是                   2分        4分

    （1）第10行第10个数是127                      4分         7分

    （2）表中第37行、38行的第1个数分别为1927，2036

    所以2008是此表中的第37行

    第2008－1927+1=82个数                         8分         14分

    （3）不存在

    第n行第1个数是

     第n+2行最后一个数是 

                         =

    这3行共有  (3n－2)+[3(n+1)－2]+[3(n+2)－2]

              =9n+3  个数                                   10分

    这3行没有数之和

                              12分

    此方程无正整数解．

    21．（理科14分，文科12分）                                            理科 文科

    （1）P（0，b）  M（a，0） 没N（x，y） 由①

         由                  ②

    将②代入①得曲线C的轨迹方程为 y2 = 4x                              5分 6分

    （2）点F′(－1，0)  ，设直线l：y = k (x+1) 代入y2 = 4x

    k2x2+2 (k2－2)x+k2=0

    由                                             7分 8分

    设A（x1，y1） B（x2，y2） D（x0，y0） 则

    故直线DE方程为

    令y=0 得   

    即的取值范围是（3，+∞）                                   10分 12分

    （3）设点Q的坐标为（－1，t），过点Q的切线为：y－t = k (x+1)

    代入y2 = 4x   消去 x整理得ky2－4y+4t+4k=0                            12分

    △=16－16k (t+k)    令

    两切线l1，l2 的斜率k1，k2是此方程的两根

    ∴k1?k2=－1    故l1⊥l2                                          14分

    22．文科：依题意                         2分

                                                     4分

              若f (x)在（－1，0）上是增函数，则在（－1，1）上

              ∵的图象是开口向下的抛物线                            6分

    ∴ 且

    解之得 t≥5                                                 12分

    理科：

    （1）

    令或                                        2分

    x        0      （0，）         （，1）    1

                   ―         0        +

        －                  －4                －3

    所以    是减函数

            是增函数                                   4分

    故时的值域为[－4，－3]                              6分

    （2）

    ∵a≥1 当时

    ∴时  g (x)↓

      时  g (x)∈[g (1)，g (0)]=[1－2a－3a2，－2a]                8分

    任给x1∈[0，1]  f (x1) ∈[－4，－3]

    存在x0∈[0，1]  使得  g (x0) = f (x1)

    则：[1－2a－3a2，－2a]=[－4，－3]                                 10分

    即 

    又a≥1  故a的取值范围为[1，]                                

     


    同步练习册答案