
题目列表(包括答案和解析)
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
(本题满分14分)如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点E为
,点E为 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: ;
;
(III)在线段AB上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出
的长;若不存在,请说明理由.
(本小题满分14分)如图所示,在四棱锥 中,
中, 平面
平面 ,
, ,
,
 ,
, ,
, 是
是 的中点.
的中点.
(1)证明: 平面
平面 ;
;
(2)若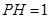 ,
, ,
, ,求二面角
,求二面角 的正切值.
的正切值.

(08年安徽皖南八校联考)(本小题满分14分)
 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
 (本小题满分14分)
(本小题满分14分)
如图所示,在侧棱垂直于底面的三棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求四棱锥A-CBB1C1的体积;
(2)证明:![]()
![]() 平面
平面![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使
![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com