
题目列表(包括答案和解析)
填空题
1.已知数列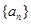 为等差数列,
为等差数列,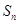 为其前
为其前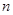 项和
项和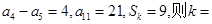
2.函数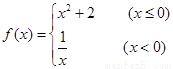 的反函数为
的反函数为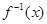 ,则
,则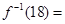 。
。
3.已知球O的表面上四点A、B、C、D,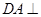 平面ABC,AB
平面ABC,AB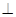 BC,DA=AB=BC=
BC,DA=AB=BC=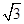 ,则球O的体积等于 。
,则球O的体积等于 。
4.某校在2010年的“八校第一次联考”中有1000人参加考试,数学考试的成绩 (
(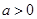 ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的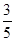 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
5.有一种数学推理游戏,游戏规则如下:

①在9×9的九宫格子中,分成9个3×3的小九格,用1到9这9个数填满整个格子;
②每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每 行每列及每个小九宫格里只能出现一次,既不能重复也不能少,那么A处应填入的数字为 ;B处应填入的数字为 。
填空题
【小题1】已知数列 为等差数列,
为等差数列, 为其前
为其前 项和
项和
【小题2】函数 的反函数为
的反函数为 ,则
,则 。
。
【小题3】已知球O的表面上四点A、B、C、D, 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。
【小题4】某校在2010年的“八校第一次联考”中有1000人参加考试,数学考试的成绩 (
( ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
【小题5】有一种数学推理游戏,游戏规则如下:
①在9×9的九宫格子中,分成9个3×3的小九格,用1到9这9个数填满整个格子;
②每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每 行每列及每个小九宫格里只能出现一次,既不能重复也不能少,那么A处应填入的数字为 ;B处应填入的数字为 。
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com