（本小题满分10分）某港口的水深（米）是时间（，单位：小时）的函数，下面是每天时间与水深的关系表：

	0	3	6	9	12	15	18	21	24
	10	13	9.9	7	10	13	10.1	7	10

经过长期观测， 可近似的看成是函数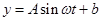

（1）根据以上数据，求出的解析式

（2）若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中的哪几段时间可以安全的进出该港？

 

 

为了了解某市工人开展体育活动的情况，拟采用分层抽样的方法从A，B，C三个区中抽取7个工厂进行调查，已知A，B，C区中分别有18，27，18个工厂

（Ⅰ）从A，B，C区中分别抽取的工厂个数；

（Ⅱ）若从抽取的7个工厂中随机抽取2个进行调查结果的对比，计算这2个工厂中至少有1个来自A区的概率.

【解析】本试题主要考查了统计和概率的综合运用。

第一问工厂总数为18+27+18=63，样本容量与总体中的个体数比为7/63=1/9…3分

所以从A，B，C三个区中应分别抽取的工厂个数为2，3，2。

第二问设A₁，A₂为在A区中的抽得的2个工厂，B₁，B₂­，B₃为在B区中抽得的3个工厂，

C₁，C₂为在C区中抽得的2个工厂。

这7个工厂中随机的抽取2个，全部的可能结果有1/2*7*6=32种。

随机的抽取的2个工厂至少有一个来自A区的结果有A₁，A₂），A₁，B₂），A₁，B₁），

A₁，B₃）A₁，C₂），A₁，C₁）， …………9分

同理A₂还能给合5种，一共有11种。  

所以所求的概率为p=11/21

 

（本小题满分12分）

在一次数学考试中，第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做每一道题的概率均为.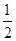

（1）求其中甲、乙两名学生选做同一道题的概率；

（2）设这4名考生中选做第22题的学生个数为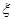，求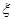的概率分布及数学期望. 的解析

 

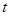某港口的水深（米）是时间（，单位：小时）的函数，下面是每天时间与水深的关系表：

	0	3	6	9	12	15	18	21	24
	10	13	9.9	7	10	13	10.1	7	10

经过长期观测， 可近似的看成是函数，（本小题满分14分）

（1）根据以上数据，求出的解析式。

（2）若船舶航行时，水深至少要11.5米才是安全的，那么船舶在一天中的哪几段时间可以安全的进出该港？

【解析】第一问由表中数据可以看到：水深最大值为13，最小值为7，，

∴A+b=13,   -A+b=7   解得  A=3,  b=10

第二问要想船舶安全，必须深度，即

∴       

解得： 得到结论。

 

 如图所示，在棱长为的正方体ABCD—A₁B₁C₁D₁中，E、F、H分

    别是棱BB₁、CC₁、DD₁的中点。

（1）求证：BH//平面A₁EFD₁；

（2）求直线AF与平面A₁EFD₁所成的角的正弦值。

 

21.（本题15分）已知函数，

   在x=1处的切线的斜率为-1，

 （1）求的解析式及单调区间；

 （2）是否总存在实数m，使得对任意的，总存在，使得

   成立？若存在，求出实数m的取值范围；若不存在，说明理由．