
题目列表(包括答案和解析)
(本题满分13分)已知向量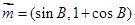 与向量
与向量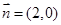 的夹角为
的夹角为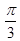 ,
,
在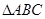 中,
中,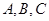 所对的边分别为
所对的边分别为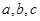 且
且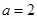 .(改编成)
.(改编成)
(I)求角B的大小;
(Ⅱ)若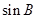 是
是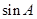 和
和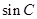 的等比中项,求
的等比中项,求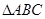 的面积。
的面积。
(本题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数学期望)
的分布列和均值(数学期望)![]() ;
;
(Ⅲ)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数学期望)达到最小,并证明之。
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数学期望)达到最小,并证明之。
(本题满分13分)在平面直角坐标系 中,抛物线C的顶点在原点,经过点
中,抛物线C的顶点在原点,经过点
A(2,2),其焦点F在 轴上.
轴上.

(Ⅰ)求抛物线C的标准方程;
(Ⅱ)求过点F,且与直线OA垂直的直线的方程.
(本题满分13分)已知二次函数 的图象经过点
的图象经过点 ,且不等式
,且不等式 对一切实数
对一切实数 都成立.
都成立.
(1)求函数 的解析式;
的解析式;
(2)若对一切 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本题满分13分) 的三个内角
的三个内角 依次成等差数列.
依次成等差数列.
(Ⅰ)若 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)若 为钝角三角形,且
为钝角三角形,且 ,求
,求
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com