（2008?上海模拟）如图a是研究小球在斜面上平抛运动的实验装置，每次将小球从弧型轨道同一位置静止释放，并逐渐改变斜面与水平地面之间的夹角θ，获得不同的射程x，最后作出了如图b所示的x-tanθ图象，则：

（1）忽略一切阻力造成的影响，在该实验中，x与tanθ的理论关系应满足x= （用v₀、g、θ表示）
（2）由图b可知，小球在斜面顶端水平抛出时的初速度v₀=．实验中发现θ超过60°后，小球将不会掉落在斜面上，则斜面的长度为m．（g取10m/s²）

（2008?上海）如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形（不计电子所受重力）．
（1）在该区域AB边的中点处由静止释放电子，求电子离开ABCD区域的位置．
（2）在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置．
（3）若将左侧电场II整体水平向右移动

L

n

（n≥1），仍使电子从ABCD区域左下角D处离开（D不随电场移动），求在电场I区域内由静止释放电子的所有位置．

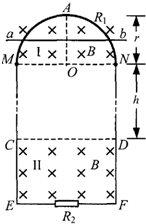（2008?上海）如图所示，竖直平面内有一半径为r、内阻为R₁、粗细均匀的光滑半圆形金属球，在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接，EF之间接有电阻R₂，已知R₁=12R，R₂=4R．在MN上方及CD下方有水平方向的匀强磁场I和II，磁感应强度大小均为B．现有质量为m、电阻不计的导体棒ab，从半圆环的最高点A处由静止下落，在下落过程中导体棒始终保持水平，与半圆形金属环及轨道接触良好，高平行轨道中够长．已知导体棒ab下落r/2时的速度大小为v₁，下落到MN处的速度大小为v₂．
（1）求导体棒ab从A下落r/2时的加速度大小．
（2）若导体棒ab进入磁场II后棒中电流大小始终不变，求磁场I和II之间的距离h和R₂上的电功率P₂．
（3）若将磁场II的CD边界略微下移，导体棒ab刚进入磁场II时速度大小为v₃，要使其在外力F作用下做匀加速直线运动，加速度大小为a，求所加外力F随时间变化的关系式．

（2008?上海）（分叉题A）某行星绕太阳运动可近似看作匀速圆周运动，已知行星运动的轨道半径为R，周期为T，万有引力恒量为G，则该行星的线速度大小为，太阳的质量可表示为．

（2008?上海模拟）在游乐场上的一个升降机中，把一重物置于台秤上，台秤与力的传感器相连，当升降机从静止加速上升，然后又匀速运动一段时间，最后停止运动；传感器的屏幕上显示出其受的压力与时间的关系（N-t）图象，如图所示，则：（g取10m/s²）
（1）该升降机在启动阶段经历了秒加速上升过程．
（2）该升降机的最大加速度是m/s²．