
题目列表(包括答案和解析)
(本小题满分12分)如图,在平面直角坐标系中,直线 :
: 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,抛物线
,抛物线 过点
过点 、点
、点 ,且与
,且与 轴的另一交点为
轴的另一交点为 ,其中
,其中 >0,又点
>0,又点![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上一动点.
上一动点.
(1)求点![]() 的坐标,并在图1中的
的坐标,并在图1中的![]() 上找一点
上找一点![]() ,使
,使![]() 到点
到点![]() 与点
与点![]() 的距离之和最小;
的距离之和最小;
(2)若△![]() 周长的最小值为
周长的最小值为![]() ,求抛物线的解析式及顶点
,求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(3)如图2,在线段![]() 上有一动点
上有一动点![]() 以每秒2个单位的速度从点
以每秒2个单位的速度从点![]() 向点
向点![]() 移动(
移动(![]() 不与端点
不与端点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ∥
∥![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() 移动的时间为
移动的时间为![]() 秒,试把△
秒,试把△![]() 的面积
的面积![]() 表示成时间
表示成时间![]() 的函数,当
的函数,当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.

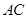 :
: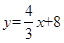 与
与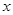 轴交于点
轴交于点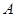 ,与
,与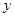 轴交于点
轴交于点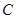 ,抛物线
,抛物线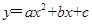 过点
过点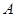 、点
、点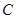 ,且与
,且与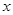 轴的另一交点为
轴的另一交点为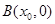 ,其中
,其中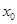 >0,又点
>0,又点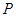 是抛物线的对称轴
是抛物线的对称轴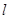 上一动点.
上一动点.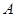 的坐标,并在图1中的
的坐标,并在图1中的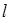 上找一点
上找一点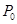 ,使
,使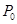 到点
到点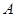 与点
与点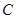 的距离之和最小;
的距离之和最小;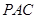 周长的最小值为
周长的最小值为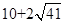 ,求抛物线的解析式及顶点
,求抛物线的解析式及顶点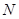 的坐标;
的坐标;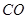 上有一动点
上有一动点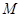 以每秒2个单位的速度从点
以每秒2个单位的速度从点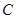 向点
向点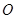 移动(
移动(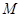 不与端点
不与端点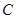 、
、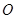 重合),过点
重合),过点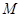 作
作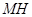 ∥
∥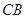 交
交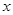 轴于点
轴于点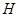 ,设
,设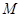 移动的时间为
移动的时间为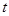 秒,试把△
秒,试把△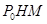 的面积
的面积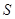 表示成时间
表示成时间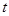 的函数,当
的函数,当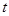 为何值时,
为何值时,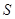 有最大值,并求出最大值.
有最大值,并求出最大值.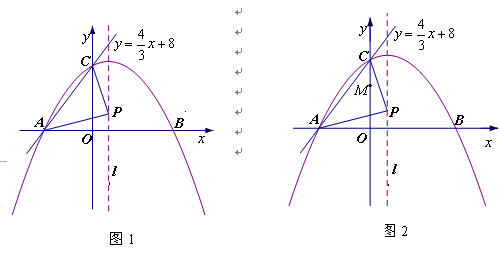
(本小题满分12分)如图,在平面直角坐标系中,直线 :
: 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,抛物线
,抛物线 过点
过点 、点
、点 ,且与
,且与 轴的另一交点为
轴的另一交点为 ,其中
,其中 >0,又点
>0,又点 是抛物线的对称轴
是抛物线的对称轴 上一动点.
上一动点.
(1)求点 的坐标,并在图1中的
的坐标,并在图1中的 上找一点
上找一点 ,使
,使 到点
到点 与点
与点 的距离之和最小;
的距离之和最小;
(2)若△ 周长的最小值为
周长的最小值为 ,求抛物线的解析式及顶点
,求抛物线的解析式及顶点 的坐标;
的坐标;
(3)如图2,在线段 上有一动点
上有一动点 以每秒2个单位的速度从点
以每秒2个单位的速度从点 向点
向点 移动(
移动( 不与端点
不与端点 、
、 重合),过点
重合),过点 作
作 ∥
∥ 交
交 轴于点
轴于点 ,设
,设 移动的时间为
移动的时间为 秒,试把△
秒,试把△ 的面积
的面积 表示成时间
表示成时间 的函数,当
的函数,当 为何值时,
为何值时, 有最大值,并求出最大值.
有最大值,并求出最大值.


如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形, M、N分别是CE、CF的中点.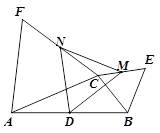
【小题1】求证:△DMN是等边三角形;
【小题2】连接EF,Q是EF中点,CP⊥EF于点P. 求证:DP=DQ.
同学们,如果你觉得解决本题有困难,可以阅读下面两位同学的解题思路作为参考:
小聪同学发现此题条件中有较多的中点,因此考虑构造三角形的中位线,添加出了一些辅助线;小慧同学想到要证明线段相等,可通过证明三角形全等,如何构造出相应的三角形呢?她考虑将△NCM绕顶点旋转到要证的对应线段的位置,由此猜想到了所需构造的三角形的位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com