
题目列表(包括答案和解析)
已知焦点在 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是 ( )
,则椭圆的方程是 ( )
A. B.
B. C.
C.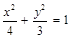 D.
D.
已知焦点在 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率
,若该椭圆的离心率 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. B.
B. C.
C. D.
D.
已知焦点在轴上、中心在原点的椭圆上一点到两焦点的距离之和为,若该椭圆的离心率,则椭圆的方程是 ( )
A. B. C. D.
已知焦点在![]() 轴上、中心在原点的椭圆上一点到两焦点的距离之和为
轴上、中心在原点的椭圆上一点到两焦点的距离之和为![]() ,若该椭圆的离心率
,若该椭圆的离心率![]() ,则椭圆的方程是( )
,则椭圆的方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知焦点在轴上、中心在原点的椭圆上一点到两焦点的距离之和为,若该椭圆的离心率,则椭圆的方程是 ( )
A. B. C. D.
一.选择题:本大题共12小题,每小题5分,共60分。
(1)A (2)B (3)B (4)A (5)D (6)D
(7)C (8)C (9)A (10)C (11)A (12)B
二.填空题:本大题共4小题,每小题5分,共20分。
(13)卷.files/image307.gif) (14)2
(15)
(14)2
(15)卷.files/image309.gif) (16)44
(16)44
三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分10分)
(Ⅰ)解法一:由正弦定理得卷.files/image311.gif) .
.
故 卷.files/image313.gif) ,
,
又 卷.files/image315.gif) ,
,
故 卷.files/image317.gif) ,
,
即 卷.files/image319.gif) ,
,
故 卷.files/image321.gif) .
.
因为 卷.files/image323.gif) ,
,
故 卷.files/image325.gif) ,
,
又 卷.files/image274.gif) 为三角形的内角,
为三角形的内角,
所以 卷.files/image328.gif) . ………………………5分
. ………………………5分
解法二:由余弦定理得 卷.files/image330.gif) .
.
将上式代入卷.files/image218.gif) 整理得
整理得卷.files/image333.gif) .
.
故 卷.files/image325.gif) ,
,
又 卷.files/image274.gif) 为三角形内角,
为三角形内角,
所以 卷.files/image328.gif) .
………………………5分
.
………………………5分
(Ⅱ)解:因为卷.files/image336.gif) .
.
故 卷.files/image338.gif) ,
,
由已知 卷.files/image222.gif) 得
得
卷.files/image341.gif)
又因为 卷.files/image343.gif) .
.
得 卷.files/image345.gif) ,
,
所以 卷.files/image347.gif) ,
,
解得 卷.files/image349.gif) . ………………………………………………10分
. ………………………………………………10分
卷.files/image237.jpg) (18)(本小题满分12分)
(18)(本小题满分12分)
(Ⅰ)证明:
∵卷.files/image228.gif) 面
面卷.files/image226.gif) ,
,卷.files/image351.gif) 面
面卷.files/image226.gif) ,
,
∴卷.files/image354.gif) .
.
又∵底面卷.files/image226.gif) 是正方形,
是正方形,
∴卷.files/image356.gif) .
.
又∵卷.files/image358.gif) ,
,
∴卷.files/image360.gif) 面
面卷.files/image235.gif) ,
,
又∵卷.files/image351.gif) 面
面卷.files/image364.gif) ,
,
∴平面卷.files/image231.gif)
卷.files/image233.gif) 平面
平面卷.files/image235.gif) . ………………………………………6分
. ………………………………………6分
(Ⅱ)解法一:如图建立空间直角坐标系卷.files/image366.gif) .
.
设卷.files/image368.gif) ,则
,则卷.files/image370.gif) ,在
,在卷.files/image372.gif) 中,
中,卷.files/image374.gif) .
.
∴卷.files/image376.gif) 、
、卷.files/image378.gif) 、
、卷.files/image380.gif) 、
、卷.files/image382.gif) 、
、卷.files/image384.gif) 、
、卷.files/image386.gif) .
.
卷.files/image387.gif) ∵
∵卷.files/image142.gif) 为
为卷.files/image242.gif) 的中点,
的中点,卷.files/image389.gif) ,
,
∴卷.files/image391.gif) .
.
设卷.files/image393.gif) 是平面
是平面卷.files/image395.gif) 的一个法向量.
的一个法向量.
卷.files/image397.gif) 则由
则由卷.files/image399.gif) 可求得
可求得卷.files/image401.gif) .
.
由(Ⅰ)知卷.files/image403.gif) 是平面
是平面卷.files/image235.gif) 的一个法向量,
的一个法向量,
且卷.files/image406.gif) ,
,
∴卷.files/image408.gif) ,即
,即卷.files/image410.gif) .
.
∴二面角卷.files/image244.gif) 的大小为
的大小为卷.files/image412.gif) . ………………………………………12分
. ………………………………………12分
解法二:
卷.files/image414.jpg) 设
设卷.files/image368.gif) ,则
,则卷.files/image370.gif) ,
,
在卷.files/image372.gif) 中,
中,卷.files/image374.gif) .
.
设卷.files/image416.gif) ,连接
,连接卷.files/image418.gif) ,过
,过卷.files/image164.gif) 作
作卷.files/image421.gif) 于
于卷.files/image423.gif) ,
,
连结卷.files/image425.gif) ,由(Ⅰ)知
,由(Ⅰ)知卷.files/image427.gif) 面
面卷.files/image429.gif) .
.
∴卷.files/image425.gif) 在面
在面卷.files/image429.gif) 上的射影为
上的射影为卷.files/image432.gif) ,
,
∴卷.files/image434.gif) .
.
故卷.files/image436.gif) 为二面角
为二面角卷.files/image438.gif) 的平面角.
的平面角.
在卷.files/image440.gif) 中,
中,卷.files/image442.gif) ,
,卷.files/image444.gif) ,
,卷.files/image446.gif) .
.
∴卷.files/image448.gif) ,
,
∴卷.files/image450.gif) .
.
∴卷.files/image452.gif) .
.
即二面角卷.files/image244.gif) 的大小为
的大小为卷.files/image412.gif) . …………………………………12分
. …………………………………12分
(19)(本小题满分12分)
解:(Ⅰ)设取到的4个球全是白球的概率卷.files/image299.gif) ,
,
则卷.files/image455.gif) .
…………………………………6分
.
…………………………………6分
(Ⅱ)设取到的4个球中红球个数不少于白球个数的概率卷.files/image457.gif) ,
,
则卷.files/image459.gif) . ………………12分
. ………………12分
(20)(本小题满分12分)
解:(I)设等比数列卷.files/image246.gif) 的首项为
的首项为卷.files/image461.gif) ,公比为
,公比为卷.files/image463.gif) ,
,
依题意,有卷.files/image465.gif) ,
,
代入卷.files/image248.gif) , 得
, 得卷.files/image467.gif) .
.
∴卷.files/image469.gif) .
…………………………………2分
.
…………………………………2分
∴卷.files/image471.gif) 解之得
解之得卷.files/image473.gif) 或
或卷.files/image475.gif) …………………6分
…………………6分
∴卷.files/image477.gif) 或
或卷.files/image479.gif) .
…………………………………8分
.
…………………………………8分
(II)又卷.files/image481.gif) 单调递减,∴
单调递减,∴卷.files/image475.gif) . …………………………………9分
. …………………………………9分
则卷.files/image483.gif) . …………………………………10分
. …………………………………10分
∴卷.files/image485.gif) ,即
,即卷.files/image487.gif) ,
,卷.files/image489.gif) ,
,
卷.files/image491.gif) .
.
故使卷.files/image493.gif) 成立的正整数n的最小值为8.………………………12分
成立的正整数n的最小值为8.………………………12分
(21)(本小题满分12分)
(Ⅰ)解:设双曲线方程为卷.files/image495.gif) ,
,卷.files/image497.gif) ,
,
由卷.files/image267.gif) ,
,卷.files/image269.gif) 及勾股定理得
及勾股定理得卷.files/image499.gif) ,
,
由双曲线定义得 卷.files/image501.gif) .
.
则卷.files/image503.gif) .
………………………………………5分
.
………………………………………5分
(Ⅱ)卷.files/image505.gif) ,
,卷.files/image507.gif)
卷.files/image509.gif) ,双曲线的两渐近线方程为
,双曲线的两渐近线方程为卷.files/image511.gif) .
.
由题意,设卷.files/image168.gif) 的方程为
的方程为卷.files/image513.gif) ,
,卷.files/image168.gif) 与
与卷.files/image515.gif) 轴的交点为
轴的交点为卷.files/image517.gif) .
.
若卷.files/image168.gif) 与
与卷.files/image519.gif) 交于点
交于点卷.files/image272.gif) ,
,卷.files/image168.gif) 与
与卷.files/image522.gif) 交于点
交于点卷.files/image274.gif) ,
,
由卷.files/image525.gif) 得
得卷.files/image527.gif) ;由
;由卷.files/image529.gif) 得
得卷.files/image531.gif) ,
,
卷.files/image533.gif) ,
,
卷.files/image535.gif) ,
,
卷.files/image537.gif) 则
则卷.files/image539.gif) ,
,
故双曲线方程为卷.files/image541.gif) .
………………………………12分
.
………………………………12分
(22)(本小题满分12分)
解:(Ⅰ)卷.files/image543.gif) ,
,
卷.files/image545.gif) .
.
又因为函数卷.files/image284.gif) 在
在卷.files/image286.gif) 上为增函数,
上为增函数,
卷.files/image547.gif) 在
在卷.files/image286.gif) 上恒成立,等价于
上恒成立,等价于
卷.files/image549.gif) 在
在卷.files/image286.gif) 上恒成立.
上恒成立.
又卷.files/image551.gif) ,
,
故当且仅当卷.files/image553.gif) 时取等号,而
时取等号,而卷.files/image555.gif) ,
,
卷.files/image557.gif) 的最小值为
的最小值为卷.files/image559.gif) .
………………………………………6分
.
………………………………………6分
(Ⅱ)由已知得:函数卷.files/image280.gif) 为奇函数,
为奇函数,
卷.files/image561.gif) ,
, 卷.files/image563.gif) , ………………………………7分
, ………………………………7分
卷.files/image565.gif) .
.
卷.files/image567.gif) 切点为
切点为卷.files/image569.gif) ,其中
,其中卷.files/image571.gif) ,
,
则切线卷.files/image168.gif) 的方程为:
的方程为:卷.files/image573.gif) ……………………8分
……………………8分
由卷.files/image575.gif) ,
,
得卷.files/image577.gif) .
.
又卷.files/image579.gif) ,
,
卷.files/image581.gif) ,
,
卷.files/image583.gif) ,
,
卷.files/image585.gif) ,
,
卷.files/image587.gif) 或
或卷.files/image589.gif) ,由题意知,
,由题意知,卷.files/image591.gif)
从而卷.files/image593.gif) .
.
卷.files/image595.gif) ,
,
卷.files/image597.gif) ,
,
卷.files/image599.gif) .
………………………………………12分
.
………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com