
题目列表(包括答案和解析)
(08年潍坊市质检)(14分)已知向量m=(a,-x),n=(ln(1+ex),a+1),![]() = m?n,
= m?n,![]() 且
且![]() 在x=1处取得极值.
在x=1处取得极值.
(1)求a的值,并判断![]() 的单调性;
的单调性;
(2)当![]() ;
;
(3)设△ABC的三个顶点A、B、C都在![]() 图象上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
图象上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
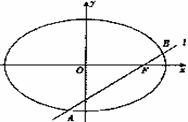
P是椭圆![]() 上一点,F1、F2分别是椭圆的左、右焦点,若|PF1|?|PF2|=12,则∠F1PF2 的大小为( )
上一点,F1、F2分别是椭圆的左、右焦点,若|PF1|?|PF2|=12,则∠F1PF2 的大小为( )
A.30° B.60° C.120° D.150°
设A(7,1),B(1,5),P(7,14)为坐标平面上三点,0为坐标原点,点M为线段OP上的一个动点.
(I)求向量![]() 在向量
在向量![]() 方向上的投影的最小值; .
方向上的投影的最小值; .
(II)当![]() ?
?![]() 取最小值时,求点M的坐标;
取最小值时,求点M的坐标;
(III)当点M满足(2)的条件和结论时,求cos∠AMB的值.
已知O、A、B三点的坐标分别为O(0,0),A(3,0),B(0,3),是P线段AB上且 ![]() =t
=t![]() (0≤t≤1)则
(0≤t≤1)则![]() ?
?![]() 的最大值为 ( )
的最大值为 ( )
A.3 B.6 C.9 D.12
已知椭圆![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
,右焦点为F(1,0),直线l经过点F,且与椭圆交于A、B两点,O为坐标原点.
(I)求椭圆的标准方程;
(II)若P是椭圆上的一个动点,求|PO|2+|PF|2的最大值和最小值;
(III)当直线l绕点F转动时,试问:在x轴上是否存在定点S,使得![]() ?
?![]() 为常数?若存在,求出定点S的坐标;若不存在,请说明理由.
为常数?若存在,求出定点S的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com