
题目列表(包括答案和解析)
(19) (本小题满分12分)(注决:在试题卷上作答无效)
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,
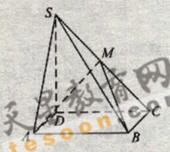
![]() ,
,![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 。
。
![]() 证明:
证明:![]() 是侧棱
是侧棱![]() 的中点;
的中点;
![]() 求二面角
求二面角![]() 的大小。
的大小。
(2010湖北理数)19(本小题满分12分)
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有![]() ?若存在,求出m的取值范围;若不存在,请说明理由。
?若存在,求出m的取值范围;若不存在,请说明理由。
(本小题满分12分)某学校共有高一、高二、高三学生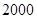 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图:
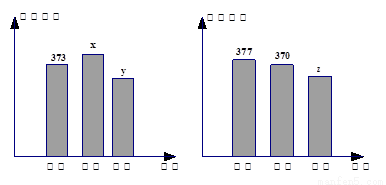
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0. 19.
(Ⅰ)求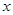 的值;
的值;
(Ⅱ)现用分层抽样的方法在全校抽取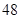 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?
(Ⅲ)已知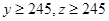 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
(本小题满分12分)根据市气象站 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(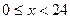 ,单位为小时,
,单位为小时,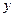 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
,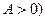 ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。
(本小题满分12分)
某初级中学有三个年级,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 370 | z | 200 |
| 男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com