
题目列表(包括答案和解析)
| |||||
对于平面内的命题:“△ABC内接于圆⊙O,圆O的半径为R,且O点在△ABC内,连结AO,BO,CO并延长分别交对边于A1,B1,C1,则AA1+BB1+CC1≥![]() ”
”
证明如下:![]()
即:![]() ,即
,即![]()
由柯西不等式,得![]()
∴AA1+BB1+CC1≥![]()
将平面问题推广到空间,就得到命题“四面体ABCD内接于半径为R的球O内,球心O在该四面体内,连结AO,BO,CO,DO并延长分别与对面交于A1,B1,C1,D1,则________”
已知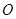 是
是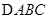 内任意一点,连结
内任意一点,连结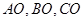 并延长交对边于
并延长交对边于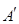 ,
,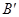 ,
,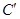 ,则
,则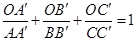 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”: 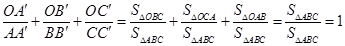 .
.
运用类比,猜想对于空间中的四面体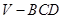 ,存在什么类似的结论,并用“体积法”证明.
,存在什么类似的结论,并用“体积法”证明.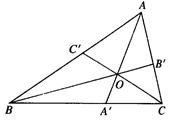
已知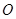 是
是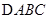 内任意一点,连结
内任意一点,连结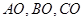 并延长交对边于
并延长交对边于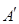 ,
,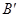 ,
,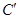 ,则
,则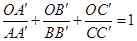 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”:
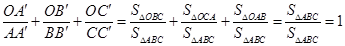 .
.
运用类比,猜想对于空间中的四面体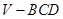 ,存在什么类似的结论,并用“体积法”证明.
,存在什么类似的结论,并用“体积法”证明.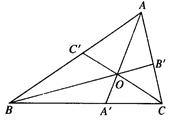
已知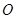 是
是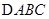 内任意一点,连结
内任意一点,连结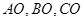 并延长交对边于
并延长交对边于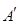 ,
,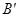 ,
,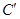 ,则
,则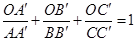 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”:
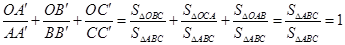 .
.
运用类比,猜想对于空间中的四面体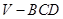 ,存在什么类似的结论,并用“体积法”证明。
,存在什么类似的结论,并用“体积法”证明。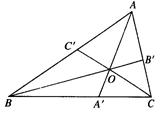
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com